Online-Rechner Trigonometrie
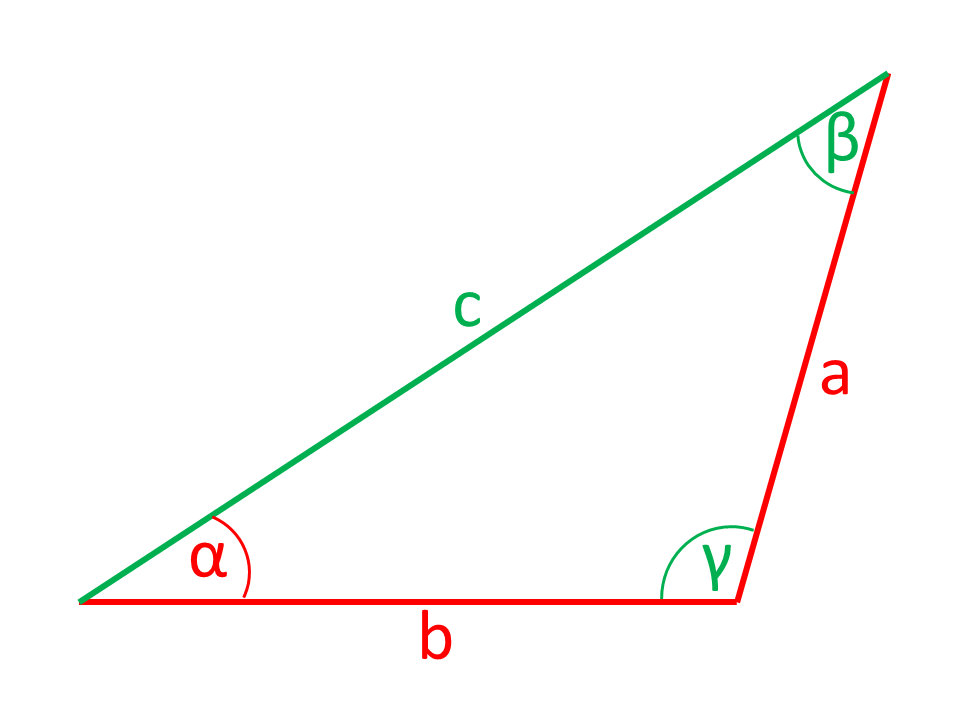
Rechner für Dreiecksberechnungen am rechtwinkligen Dreieck
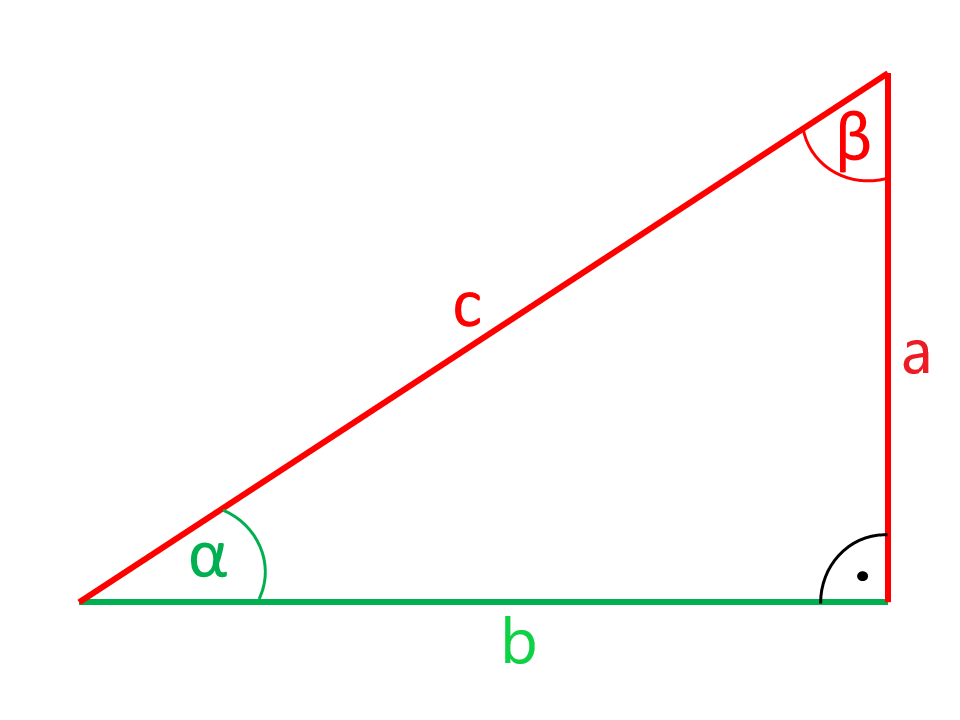
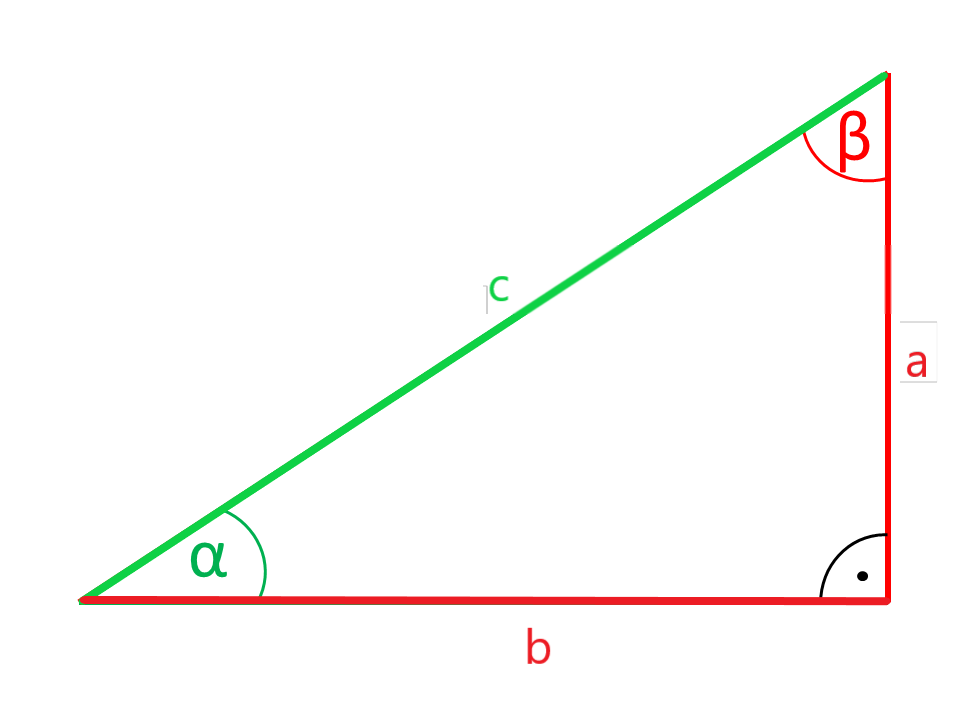
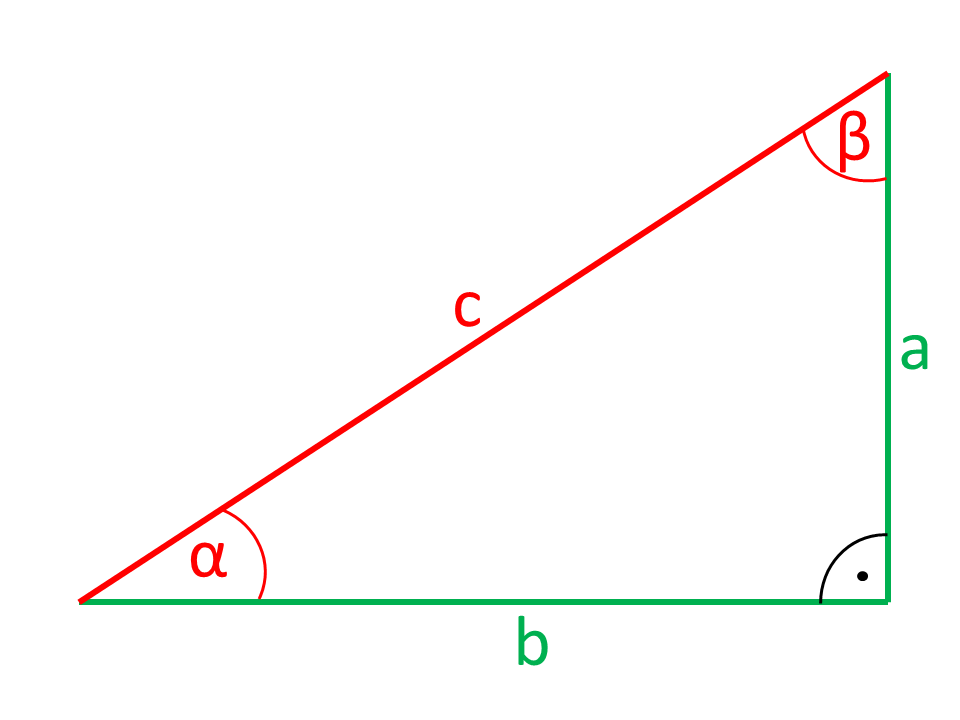
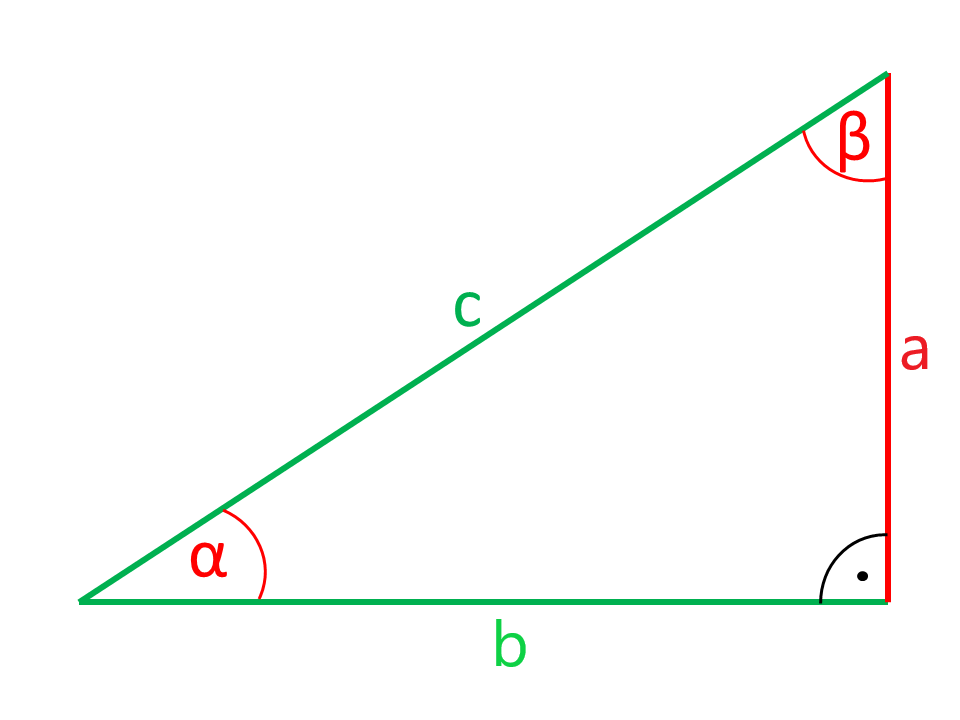
Die in den Abbildungen rot eingezeichneten Seiten bzw. Winkel werden aus den grün eingezeichneten Seiten und Winkeln berechnet.
Gegeben: Winkel und Gegenkathete
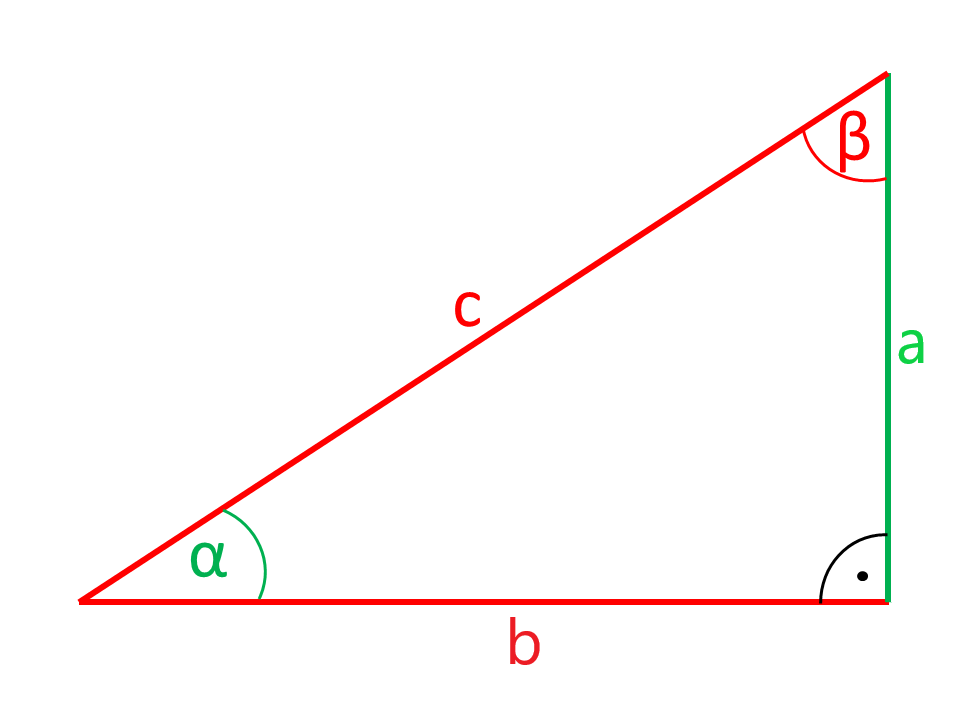
Rechner für Dreiecksberechnungen am allgemeinen (schiefwinkligen) Dreieck
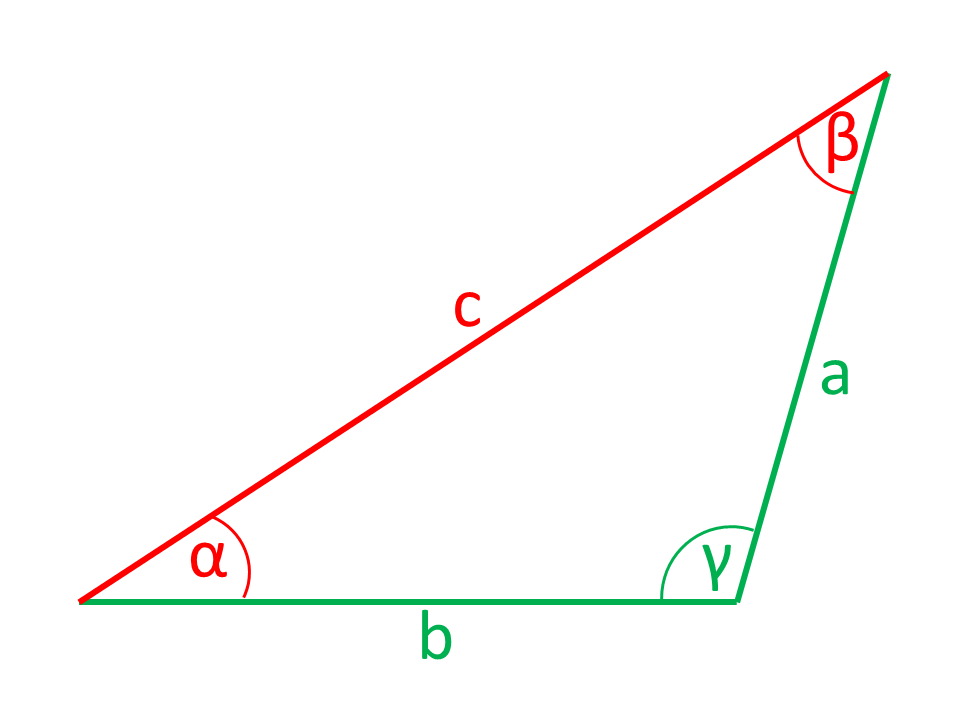
Die in den Abbildungen rot eingezeichneten Seiten bzw. Winkel werden aus den grün eingezeichneten Seiten und Winkeln berechnet.
Gegeben: Zwei Seiten und ein Winkel
Gegeben: Drei Seiten
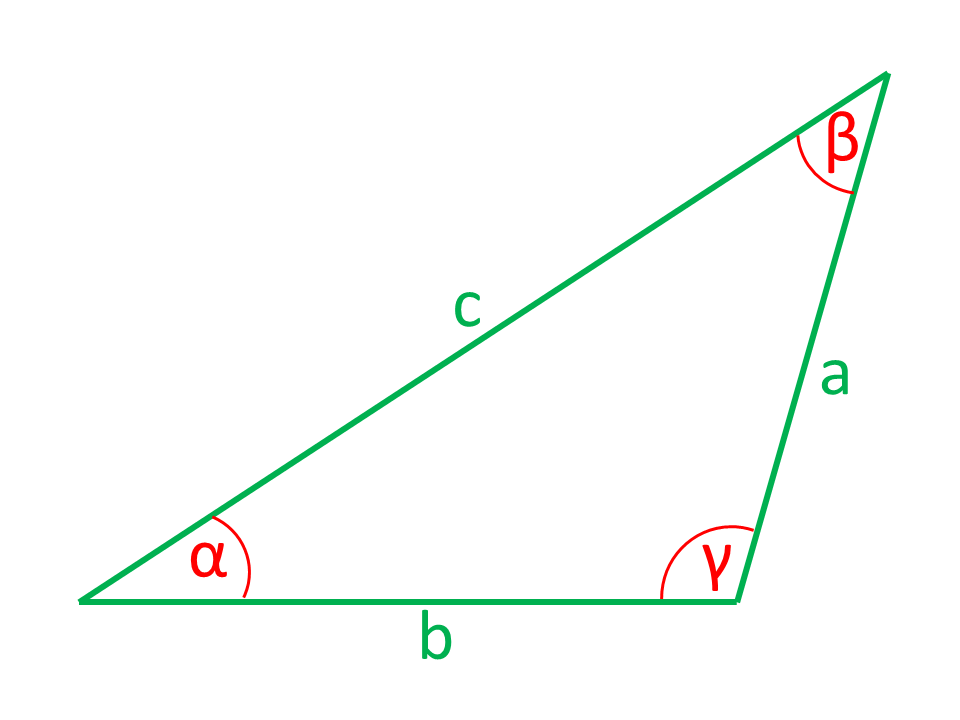
Beispiele für die Anwendung trigonometrischer Berechnungen
Im folgenden einige exemplarische Beispiele, die die Anwendung der trigonometrischen Formeln illustrieren.
Beispiel: Berechnung der Turmhöhe
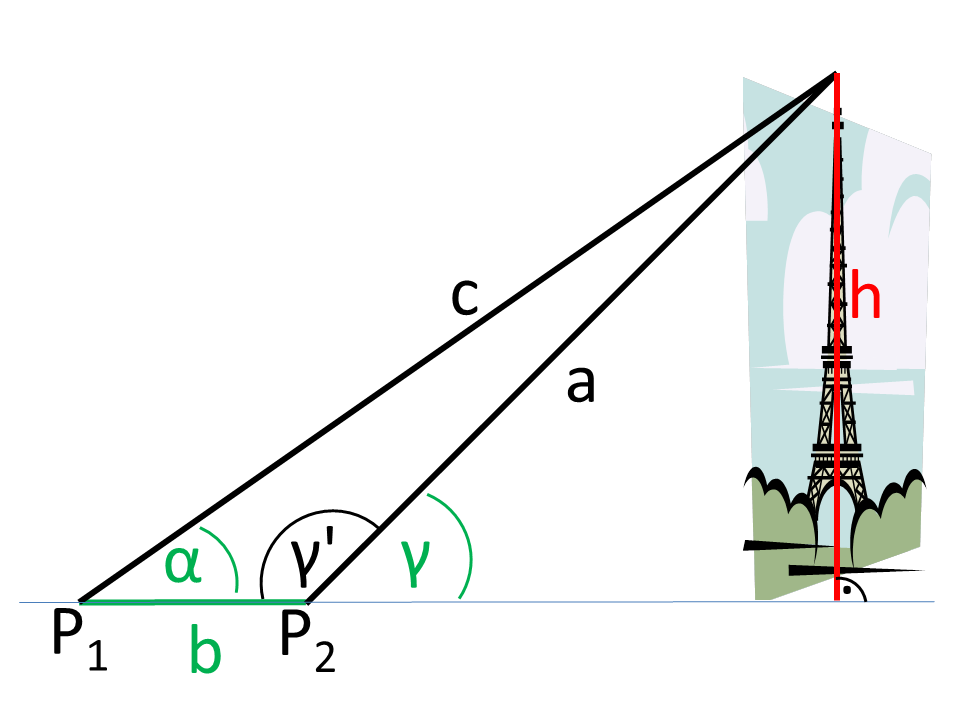
Das Beispiel zeigt, wie eine Höhe ermittelt werden kann, auch dann, wenn ein direkter Zugang nicht möglich ist.
Die Abbildung zeigt, dass aus zwei Positionen (P1, P2) die Sichtwinkel (α, γ) und der Abstand b der Positionen ermittelt wurden (Grün in der Abbildung).
Ein Dreieck wird aus P1, P2 und der Turmspitze gebildet. Von diesem allgemeinen Dreieck sind der Winkel α und die Seite b bekannt. Der Winkel γ' kann folgendermaßen berechnet werden:
Der noch fehlende Winkel β kann ermittelt werden, da die Winkelsumme im Dreieck 180° beträgt.
Im nächsten Schritt wird der Sinussatz verwendet um die Seite a zu berechnen. Die Seite a ist eine gemeinsame Seite von dem allgemeinen Dreieck und dem rechtwinkligen Dreieck das aus a und der Höhe des Turms sowie der Grundlinie gebildet wird.
In dem rechtwinkligen Dreieck ist a die Hypotenuse und h die Gegenkathete des Winkels γ. Die gesuchte Höhe h läßt sich also mit der Winkelfunktion berechnen.
Alternativ kann die Turmhöhe auch berechnet werden, wenn man zwei Gleichungen für die rechtwinkligen Dreiecke ansetzt. Das erste Dreieck ergibt sich aus P1 und dem Fusspunkt des Turms sowie der Turmspitze. Das zweite analog ausgehend aber von P2.
Es gilt:
und
mit der unbekannten Strecke x von P2 zum Fusspunkt des Turms.
Umformen der Gleichungen ergibt jeweils:
und
Gleichsetzen der Gleichungen und Auflösen nach h ergibt die Lösung:
Das die beiden Lösungen für h äquivalent sind kann man leicht nachweisen, indem man
und
ersetzt.
Mit dem Additionstheorem
ergibt sich die obige Lösung.
Es ist also
Rechner zur Berechnung der Turmhöhe
Eingabe der Sichtwinkel und des Abstands:
Beispiel: Kreuzpeilung
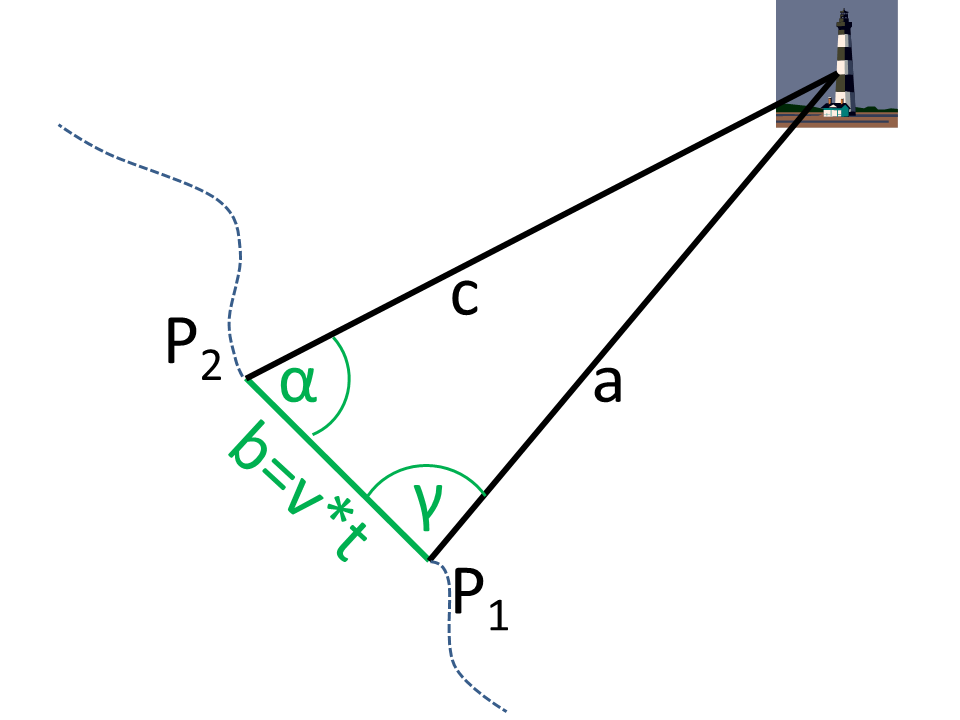
Bei der Kreuzpeilung wird ein fester Punkt (z.B. ein Leuchtturm) von zwei Positionen aus angepeilt. Zwischen den beiden Peilungen (P1, P2) wird ein konstanter Kurs und eine konstante Geschwindigkeit gefahren. Dann kann aus den Peilungen der Abstand zum angepeilten Punkt bestimmt werden.
Die Abbildung zeigt, dass an zwei Positionen (P1, P2) die Sichtwinkel (α, γ) relativ zur Fahrtrichtung ermittelt wurden (Grün in der Abbildung). Die Seitenlänge b ergibt sich aus der Geschwindigkeit v und dem zeitlichen Abstand t der Messungen.
Ein Dreieck wird aus P1, P2 und dem angepeilten Punkt (Leuchtturm) gebildet. Von diesem allgemeinen Dreieck sind der Winkel α und die Seite b = v * t bekannt.
Der noch fehlende Winkel β kann ermittelt werden, da die Winkelsumme im Dreieck 180° beträgt.
Im nächsten Schritt wird der Sinussatz verwendet um die Seite a zu berechnen. Die Seite a ist ist der Abstand zum Messpunkt P1.
Der Abstand zum zweiten Messpunkt wird analog berechnet.
Beispiel: Messung einer unzugänglichen Strecke (Hansensche Aufgabe)
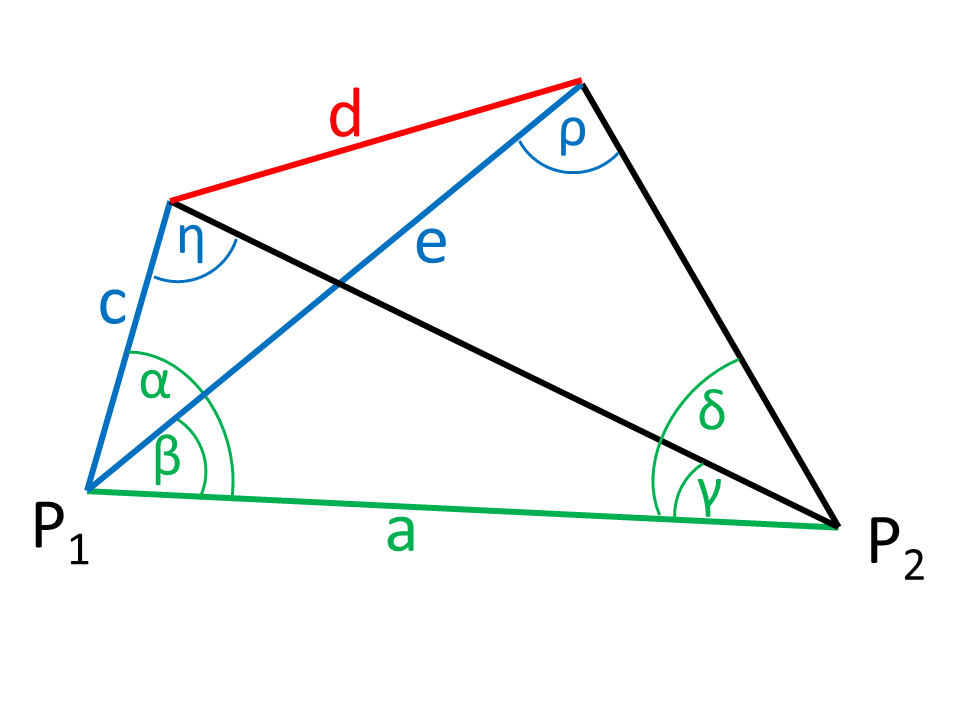
Um eine unzugängliche Strecke zu vermessen werden Anfang und Ende der Strecke von zwei Punkten (P1, P2) aus angepeilt.
Die Abbildung zeigt, dass an zwei Positionen (P1, P2) die Sichtwinkel (α, β, γ, δ) auf Anfang und Ende der Strecke relativ zur Verbindungsachse der Punkte ermittelt wurden (Grün in der Abbildung). Der Abstand a der Messpunkte ist ebenfalls bekannt. Zu ermitteln ist die Länge der unzugänglichen Strecke d (Rot in der Abbildung).
In der Abbildung sind die zu berechnenden Zwischenwerte Blau eingezeichnet.
Der Winkel η kann ermittelt werden, da die Winkelsumme im Dreieck 180° beträgt.
Im nächsten Schritt wird der Sinussatz verwendet um die Seite c zu berechnen.
Die Seite e wird auch mit dem Sinussatz berechnet.
Der Winkel ρ ergibt sich aus der Winkelsumme im Dreieck.
Mit dem Kosinussatz kann jetzt die gesuchte Strecke d berechnet werden.
Beispiel: Kräftedreieck am Pendel
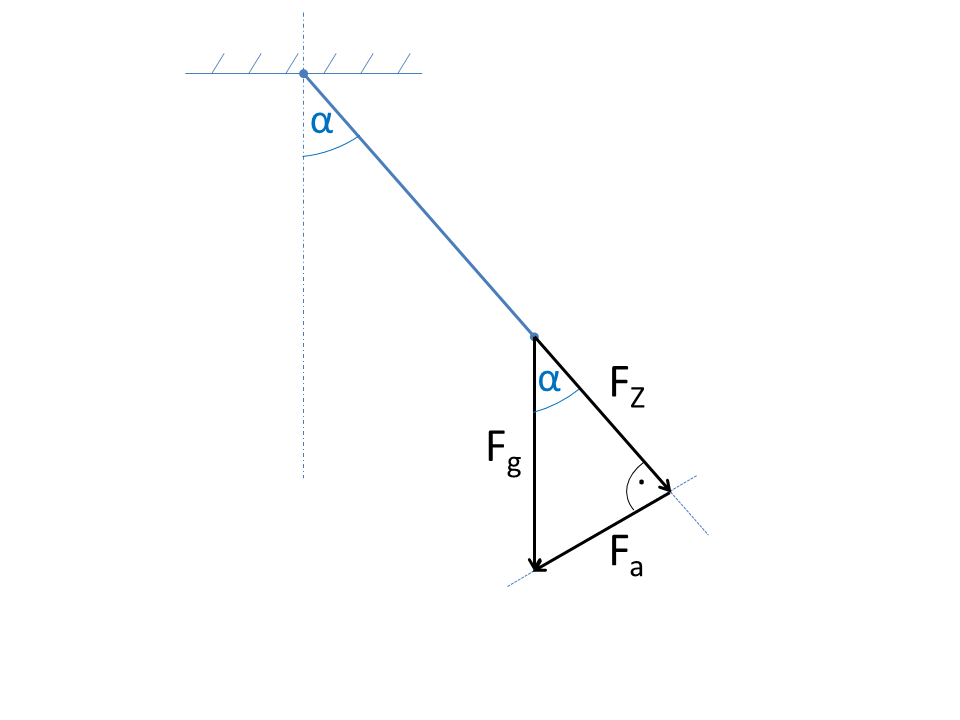
Die Zerlegung von Kräften in orthogonale Komponenten spielt in der Mechanik eine wichtige Rolle. In diesem Beispiel wird gezeigt, wie die Gewichtskraft mittels der Winkelfunktionen in zwei Komponenten zerlegt werden kann.
Die Abbildung zeigt ein Fadenpendel mit einer Masse am Ende des Fadens. Die Gewichtskraft Fg soll in Teilkräfte zerlegt werden. Die Kraft in Richtung des Fadens FZ trägt nicht zur Beschleunigung bei und es ist daher für die Bewegungsgleichung relevant die Kraft Fa zu Wissen.
Die Teilkräfte können, da es sich um ein rechtwinkliges Dreieck handelt, direkt über die Winkelfunktionen angegeben werden.
Trigonometrie allgemein
Die Grundaufgabe der Trigonometrie besteht darin, aus drei Größen eines gegebenen Dreiecks (Seitenlängen, Winkelgrößen, Längen von Dreieckstransversalen usw.) andere Größen dieses Dreiecks zu berechnen. Als Hilfsmittel werden die trigonometrischen Funktionen Sinus (sin), Kosinus (cos), Tangens (tan), Kotangens (cot). Vorläufer der Trigonometrie gab es bereits während der Antike in der griechischen Mathematik. Aristarchos von Samos nutzte die Eigenschaften rechtwinkliger Dreiecke zur Berechnung der Entfernungsverhältnisse zwischen Erde und Sonne bzw. Mond.
Rechtwinkliges Dreieck
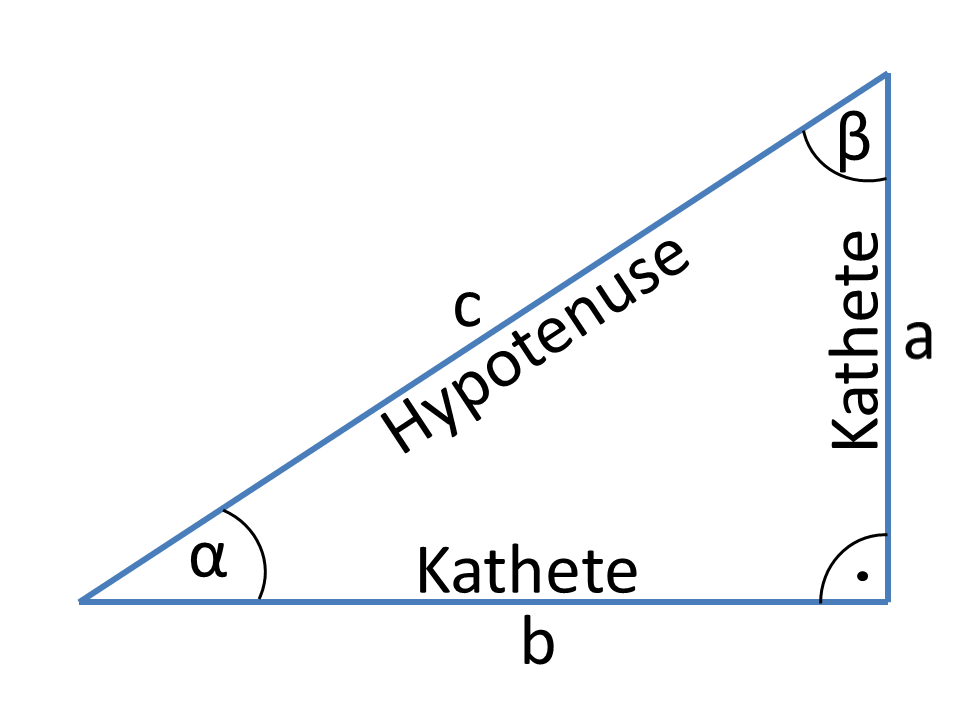
Definitionen
Die Seiten a und b des rechtwinkligen Dreiecks, die den rechten Winkel einschließen sind die Katheten. Die dem rechten Winkel gegenüber liegende Seite c ist die Hypotenuse. Betrachtet man den Winkel α so ist die Seite a die Ankathete und b die Gegenkathete.
Winkelfunktionen
Grad / Radiant
Der Winkel kann in Grad (deg) oder im Bogenmaß (rad) angegeben werden. Der Vollkreis in Grad ist 360 Grad, im Bogenmaß sind es 2π. Dementsprechend gelten die folgenden Umrechnungen.
Winkelsumme
Die Winkelsumme im Dreieck beträgt 180°. Damit gilt im rechwinkligen Dreieck folgende Beziehung für die Winkel.
Allgemeines (schiefwinkliges) Dreieck
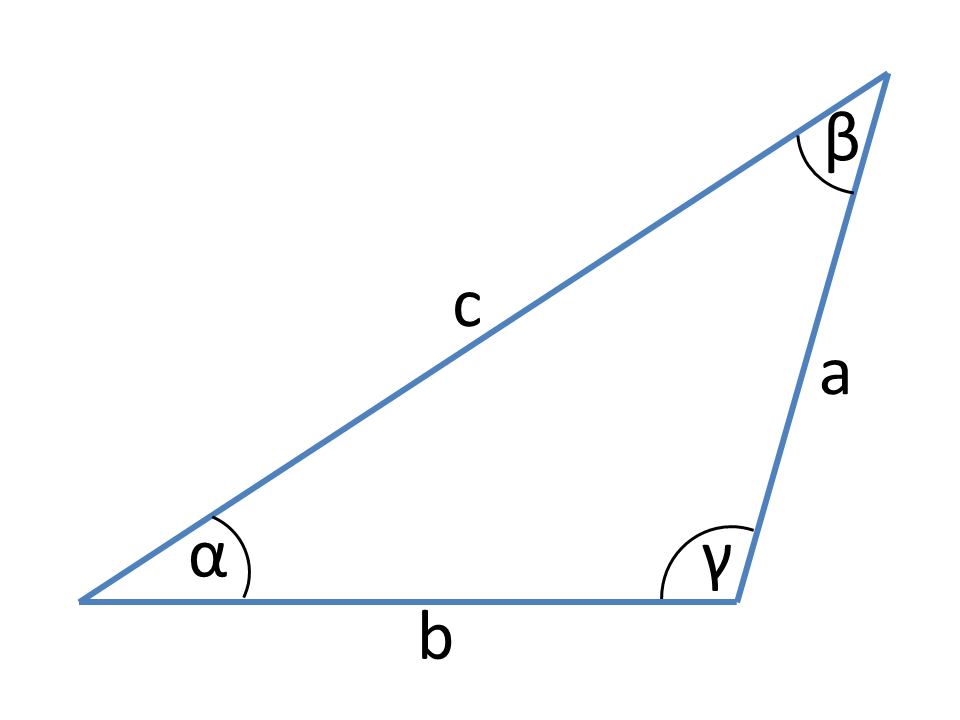
Definitionen
Wesentlich für die Berechnungen im allgemeinen Dreieck sind der Kosinus- und der Sinussatz sowie die Beziehungen der Winkelfunktionen.
Sinussatz
Kosinussatz
Projektionssatz
Tangensformel
Winkelsumme
Die Winkelsumme im Dreieck beträt 180°.
Umkreisradius r
mit
Inkreisradius ρ
Höhe hc auf c
Fläche A
Heronische Flächenformel
Eigenschaften trigonometrischer Funktionen
Reduktionsformeln (in Grad)
Zusammhang der trigonometrischen Funktionen bei gleichem Argument
Additionstheoreme der trigonometrischen Funktionen
Weitere Seiten zum Thema
Hier einige weitere Seiten:
Index Dreieck Tabellen trigonometrischer Funktionen n-fache Argumente und Potenzen trigonometrischer Funktionen Funktionswerte sin, cos, tan und arc