Online Dreiecksrechner

Interaktive Dreiecksberechnungen

Dreiecksrechner zur Berechnung der Winkel, Seiten, Höhen, Winkelhalbierenden und Seitenhalbierenden am allgemeinen Dreieck. Berechnung und grafische Darstellung des Inkreises und des Umkreises.

Eingabe des Dreiecks entweder mittels der Eingabe der Eckpunkte in den numerischen Feldern oder durch das Ziehen der Eckpunkte in der Grafik. Die berechneten Werte sind in der Tabelle aufgelistet. Die Berechnungsformeln für die Dreiecksberechnungen sind unten.

⃢

↹#.000

🔍↔

🔍↕

Seitenlängen:

Höhen:

h_a=

h_b=

h_c=

Winkel in Grad:

α=

β=

γ=

Winkels in Radiant:

α=

β=

γ=

Seitenhalbierende:

m_a=

m_b=

m_c=

Winkelhalbierende:

l_α=

l_β=

l_γ=

Umfang U=

Fläche =

Kreisradien

Wertebereich der Achsen

x-min=

x-max=

y-min=

y-max=

Definition des Dreiecks:

Punktkoordinaten P1 x, y

P1=

Punktkoordinaten P2 x, y

P2=

Punktkoordinaten P3 x, y

P3=

Seitenlängen

Winkel

α=

β=

γ=

Styles für die Darstellung und Auswahl der angezeigten Elemente:

P₁, P₂, P₃:

Seiten:

Inkreis:

Umkreis:

Höhen:

Seitenhalbierenden:

Mittelsenkrechte:

Winkelhalbierende:

Berechnungsformeln für das Dreieck

Winkelsumme

Die Winkelsumme im Dreieck beträgt 180°.

$α + β + γ = 180 °$

Seitenhalbierende (Median)

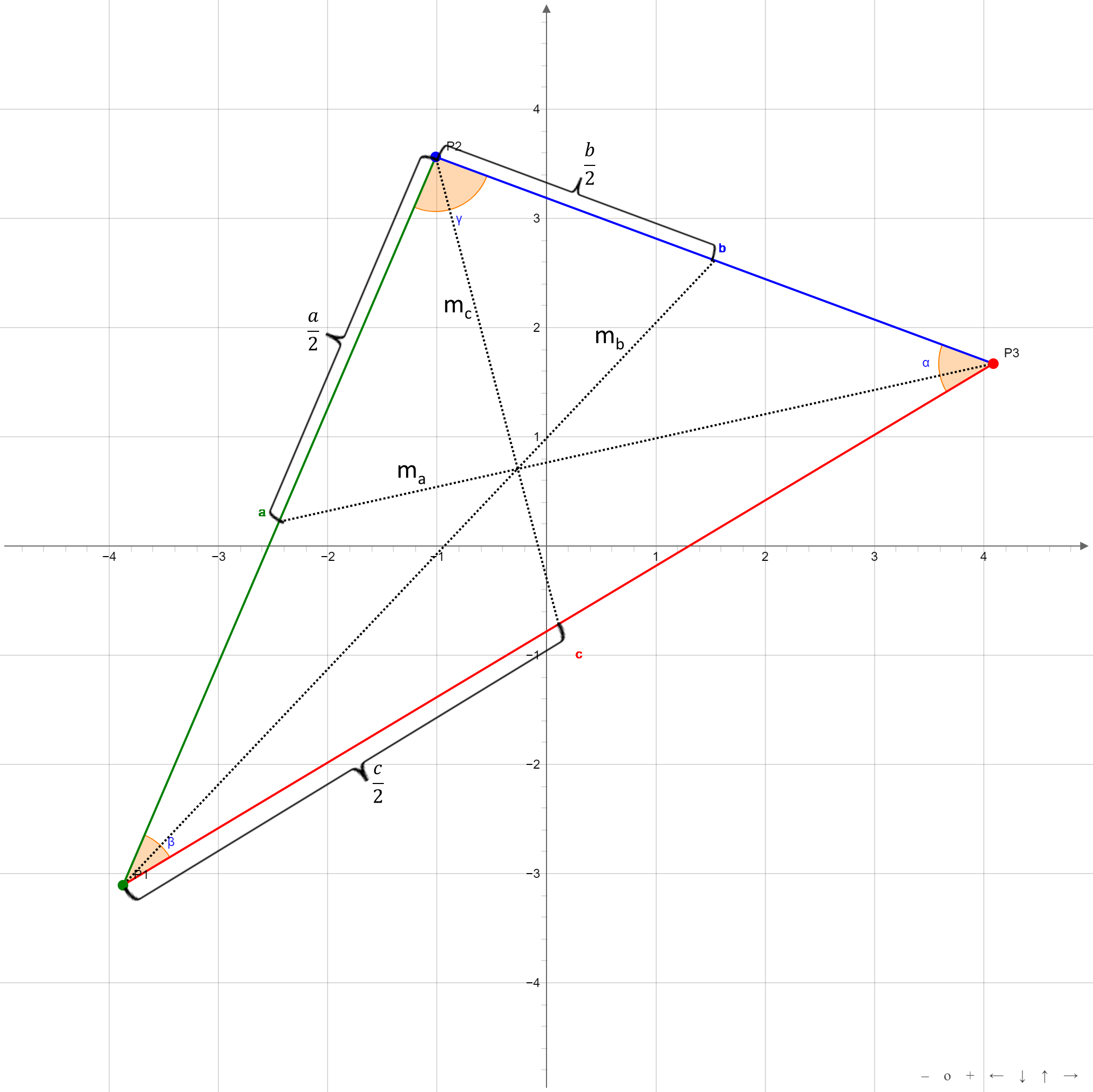
Unter einer Seitenhalbierenden versteht man eine Gerade, die einen Eckpunkt des Dreiecks mit der Mitte der gegenüberliegenden Seite verbindet. Die Seitenhalbierenden eines Dreiecks schneiden sich im Schwerpunkt des Dreiecks.

Die Länge der Seitenhalbierenden der Seite a ist:

$m_{a} = \frac{\sqrt{2 (b^{2} + c^{2}) - a^{2}}}{2}$

Die Länge der Seitenhalbierenden der Seite b ist:

$m_{b} = \frac{\sqrt{2 (a^{2} + c^{2}) - b^{2}}}{2}$

Die Länge der Seitenhalbierenden der Seite c ist:

$m_{c} = \frac{\sqrt{2 (a^{2} + b^{2}) - c^{2}}}{2}$

Winkelhalbierende

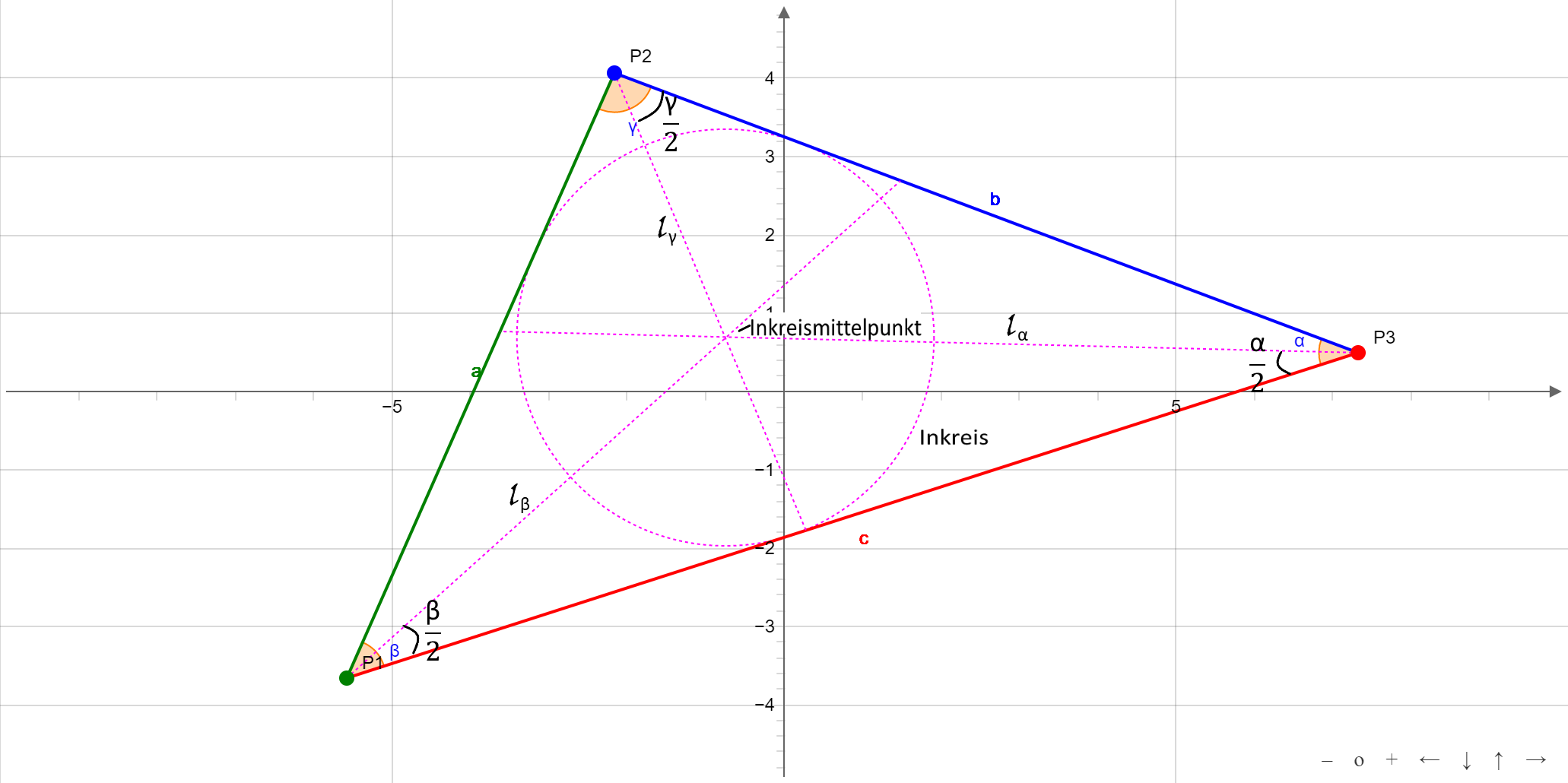
Unter einer Winkelhalbierenden versteht man eine Gerade, die einen Winkel des Dreiecks in zwei gleiche Teile teilt. Die Winkelhalbierenden eines Dreiecks schneiden sich im Mittelpunkt des Inkreises.

Die Länge der Winkelhalbierenden des Winkels α ist:

$l_{α} = \frac{\sqrt{b c {(b + c)}^{2} - a^{2}}}{b + c}$

Die Länge der Winkelhalbierenden des Winkels β ist:

$l_{β} = \frac{\sqrt{a c {(a + c)}^{2} - b^{2}}}{a + c}$

Die Länge der Winkelhalbierenden des Winkels γ ist:

$l_{γ} = \frac{\sqrt{b a {(b + a)}^{2} - c^{2}}}{b + a}$

Höhen

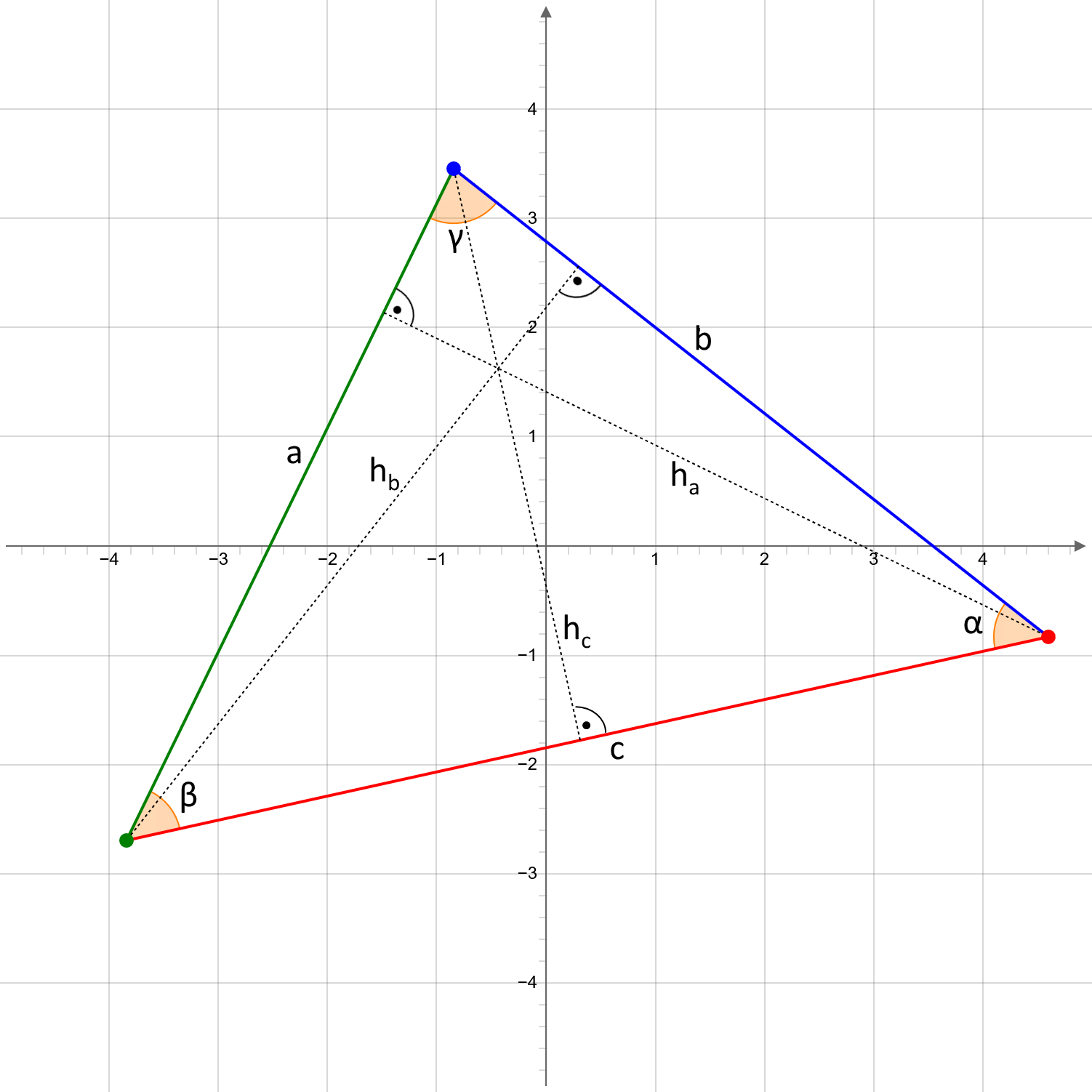
Unter der Höhe versteht man eine Gerade, die senkrecht (unter 90°) auf einer Seite steht und die Seite mit dem gegenüberliegenden Eckpunkt verbindet.

Die Länge der der Höhe auf der Seite a ist:

$h_{a} = b \cdot \sin (γ) = c \cdot \sin (β)$

Die Länge der der Höhe auf der Seite b ist:

$h_{b} = a \cdot \sin (γ) = c \cdot \sin (α)$

Die Länge der der Höhe auf der Seite c ist:

$h_{c} = a \cdot \sin (β) = b \cdot \sin (α)$

Mittelsenkrechte

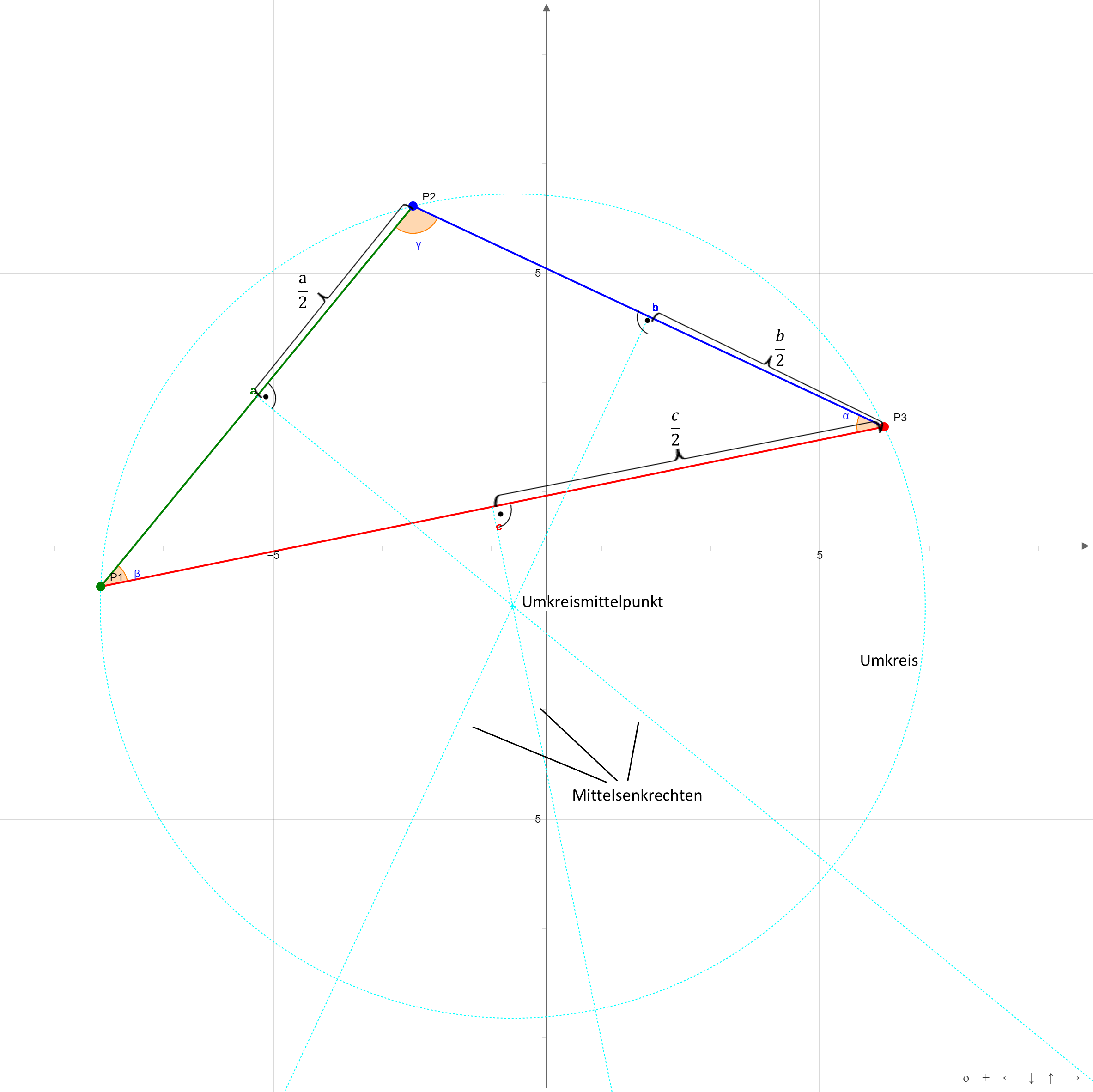
Unter einer Mittelsenkrechten versteht man eine Gerade, die eine Seite des Dreiecks in zwei gleiche Teile teilt und senkrecht auf der Seite steht. Die Mittelsenkrechten eines Dreiecks schneiden sich im Mittelpunkt des Umkreises.

Umkreisradius r

Der Umkreis ist ein Kreis, der durch die Eckpunkte des Dreiecks geht.

$r = \frac{s}{4 \cdot \cos (\frac{α}{2}) \cdot \cos (\frac{β}{2}) \cdot \cos (\frac{γ}{2})}$

mit

$s = \frac{1}{2} (a + b + c)$

Inkreisradius ρ

Der Inkreis ist ein Kreis, der jede Seite des Dreiecks berührt (tangiert).

$ρ = \sqrt{\frac{(s - a) (s - b) (s - c)}{s}}$

Dreiecksfläche F

Berechnungsformel für die Dreiecksfläche:

$F = \frac{1}{2} a \cdot b \cdot \sin (γ)$

Dreiecksumfang U

Berechnungsformel für den Dreiecksumfang:

$U = a + b + c$

Heronische Flächenformel

Berechnungsformel nach Heron für die Dreiecksfläche:

$F = ρ s = \sqrt{s (s - a) (s - b) (s - c)}$

Mittellinie

Die Mittellinie verbindet die Mittelpunkte zweier Dreiecksseiten. Sie ist parallel zu der dritten Seite und halb so lang.

Rechtwinkliges Dreieck

Die Katheten a und b bilden einen rechten Winkel. Dem rechten Winkel gegenüber liegt die Hypotenuse c. Es gilt der Satz des Pythagoras:

$c^{2} = a^{2} + b^{2}$

Fläche F im rechtwinkligen Dreieck

Berechnungsformel für die Dreiecksfläche im rechtwinkligen Dreieck:

$F = \frac{a \cdot b}{2}$

Wesentlich für die Berechnungen am allgemeinen Dreieck sind der Sunus- und der Kosinussatz.

Sinussatz

$\frac{a}{\sin (α)} = \frac{b}{\sin (β)} = \frac{c}{\sin (γ)}$

Kosinussatz

$a^{2} = b^{2} + c^{2} - 2 b c \cos (α)$

$b^{2} = a^{2} + c^{2} - 2 a c \cos (β)$

$c^{2} = a^{2} + b^{2} - 2 a b \cos (γ)$

Screenshot des Diagramms

Drucken oder speichern des Bildes mittels rechter Maustaste.

Weitere Seiten

Liste weiterer Seiten:

Index Trigonometrie Tabellen trigonometrischer Funktionen n-fache Argumente und Potenzen trigonometrischer Funktionen Kreis Rechteck Parallelogramm Ellipse