Scheitelpunktform

Rechner für die Umrechnung in die Scheitelpunktform

Der Rechner ermittelt schrittweise die Scheitelpunktform der quadratischen Funktion.

Die allgemeine quadratischen Funktion

$y (x) = a x^{2} + b x + c$

wird in die Scheitelpunktform umgeformt

$y (x) = a {(x - x_{S})}^{2} + y_{S}$

Eingabe der Koeffizienten a, b und c der quadratischen Funktion:

Umformung in die Scheitelpunktform mit quadratischer Ergänzung:

Ergebnis ist die Scheitelpunktform:

Die Scheitelpunktform der quadratischen Funktion lautet:

$y (x) = a {(x - x_{S})}^{2} + y_{S}$

oder wenn die quadratische Funktion in Normalform d.h. a=1 vorliegt:

$y (x) = {(x - x_{S})}^{2} + y_{S}$

Dabei sind x_S und y_S die x- und y-Koordinate des Scheitelpunkts der Parabel. Der Scheitelpunkt bezeichnet das Minimum oder Maximum der Funktion je nachdem ob die Parabel nach oben oder unten geöffnet ist.

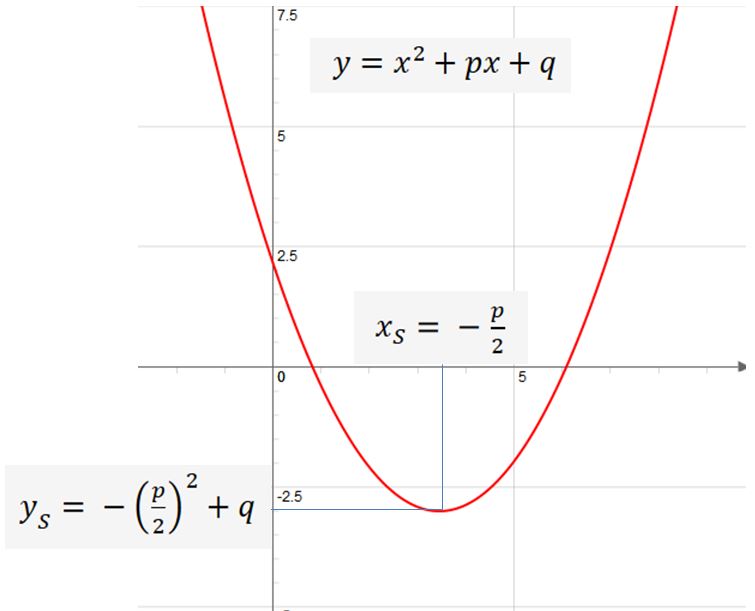
Scheitelpunkt in p,q-Form

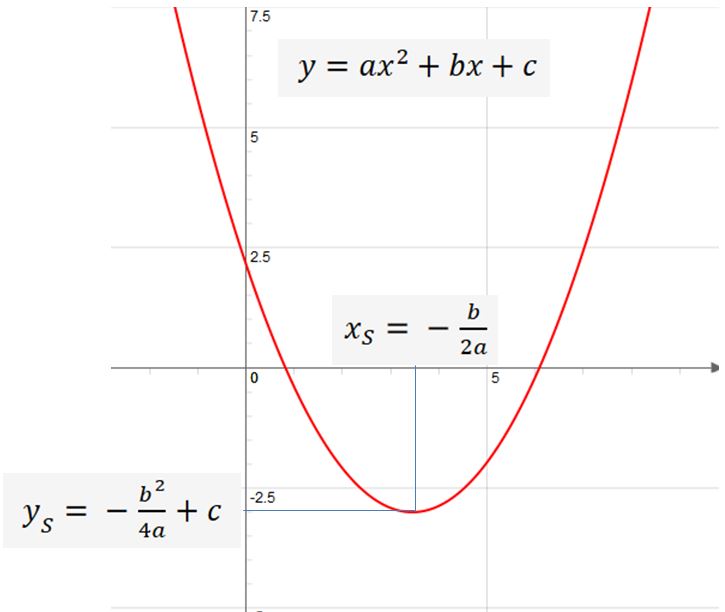
Scheitelpunkt in allgemeiner Form

Scheitelpunkt der Parabel

Die Bestimmung des Scheitelpunkts einer quadratischen Funktion erfolgt mittels der Ableitung der Funktion. Bedingung für ein Extremum ist, dass die erste Ableitung der Funktion verschwindet. Bei einer quadratischen Funktion ist das hinreichend für ein Minimum oder Maximum.

Ausgangspunkt ist die allgemeine Form der quadratischen Funktion:

$y (x) = a x^{2} + b x + c$

Die Ableitung der allgemeinen Form lautet:

$y' = 2 a x + b$

Die Bedingung für den Scheitelpunkt ist, dass die Ableitung verschwindet. D.h. es gilt folgende Gleichung:

$2 a x + b = 0$

Auflösen der Gleichung nach x ergibt die x-Koordinate des Scheitelpunkts:

$x_{S} = - \frac{b}{2 a}$

Einsetzen in die allgemeine quadratische Funktion liefert die y-Koordinate des Scheitelpunkts:

$y_{S} = - \frac{b^{2}}{4 a} + c$

Aus der zweiten Ableitung der quadratischen Funktion folgt ob der Scheitelpunkt ein Maximum oder ein Minimum der Parabel ist. Die zweite Ableitung lautet:

$y'' = 2 a$

Daher ist für a > 0 der Scheitelpunkt ein Minimum der Parabel und für a < 0 ein Maximum.

Umformung von der Normalform zur Scheitelpunktform

In der Normalform ist der Koeffizient vor x² gleich 1. Die Normalform der quadratischen Funktion mit den konstanten Koeffizienten p und q lautet:

$y (x) = x^{2} + p x + q$

Liegt die quadratischen Funktion in Normalform vor ist der Scheitelpunkt gegeben durch:

$x_{S} = - \frac{p}{2}$

$y_{S} = - {(\frac{p}{2})}^{2} + q$

Umformung von der Normalform zur Scheitelpunktform mit quadratischer Ergänzung und Anwendung des ersten Binoms:

$x^{2} + p x + q =$

$x^{2} + p x + {(\frac{p}{2})}^{2} - {(\frac{p}{2})}^{2} + q =$

${(x + \frac{p}{2})}^{2} - {(\frac{p}{2})}^{2} + q =$

${(x - \frac{- p}{2})}^{2} - {(\frac{p}{2})}^{2} + q =$

${(x - x_{S})}^{2} + y_{S}$

Rechner für die Umrechnung von der Normalform in die Scheitelpunktform

Eingabe der Koeffizienten p und q der quadratischen Gleichung:

Umformung in die Scheitelpunktform mit quadratischer Ergänzung:

Umformung von der allgemeinen Form zur Scheitelpunktform

Allgemeine Form der quadratischen Funktion mit den konstanten Koeffizienten a, b und c:

$y = a x^{2} + b x + c$

Liegt die quadratischen Funktion in der allgemeinen Form vor ist der Scheitelpunkt gegeben durch:

$x_{S} = - \frac{b}{2 a}$

$y_{S} = - \frac{b^{2}}{4 a} + c$

Umformung von der allgemeinen Form zur Scheitelpunktform mit quadratischer Ergänzung und Anwendung des ersten Binoms:

$a x^{2} + b x + c =$

$a (x^{2} + \frac{b}{a} x) + c =$

$a (x^{2} + \frac{b}{a} x + {(\frac{b}{2 a})}^{2} - {(\frac{b}{2 a})}^{2}) + c =$

$a (x^{2} + \frac{b}{a} x + {(\frac{b}{2 a})}^{2}) - \frac{b^{2}}{4 a} + c =$

$a {(x + \frac{b}{2 a})}^{2} - \frac{b^{2}}{4 a} + c =$

$a {(x - \frac{- b}{2 a})}^{2} - \frac{b^{2}}{4 a} + c$

$a {(x - x_{S})}^{2} + y_{S}$

Von der Scheitelpunktform zur allgemeinen Form

Umformung der Scheitelpunktform der quadratischen Funktion in die allgemeine Form.

Ausgangspunkt ist die Scheitelpunktform

$y = a {(x - x_{S})}^{2} + y_{S} =$

Auflösen des Quadrats ergibt:

$a (x^{2} - 2 x x_{S} + {x_{S}}^{2}) + y_{S} =$

Ausmultiplizieren der Klammer ergibt:

$a x^{2} - 2 a x x_{S} + a {x_{S}}^{2} + y_{S} =$

Einsetzen der von x_S und y_S ergibt:

$a x^{2} + 2 a x \frac{b}{2 a} + a {(- \frac{b}{2 a})}^{2} - \frac{b^{2}}{4 a} + c =$

Kürzen ergibt:

$a x^{2} + b x + \frac{b^{2}}{4 a} - \frac{b^{2}}{4 a} + c =$

Die Summanden heben sich auf und es folgt die allgemeine quadratische Funktion:

$a x^{2} + b x + c$

Berechnung der Nullstellen aus der Scheitelpunktform

Aus der Scheitelpunktform ist es einfach die Nullstellen der quadratischen Funktion zu bestimmen.

Ausgangspunkt ist die Scheitelpunktform

$y = a {(x - x_{S})}^{2} + y_{S}$

mit der Bedingung, dass die Funktion Null sein muss

$0 = a {(x - x_{S})}^{2} + y_{S}$

Umformung ergibt

${(x - x_{S})}^{2} = - \frac{y_{S}}{a}$

und die Quadratwurzel ergibt

$x - x_{S} = \pm \sqrt{- \frac{y_{S}}{a}}$

und damit schließlich die Nullstellen

$x_{1,2} = x_{S} \pm \sqrt{- \frac{y_{S}}{a}}$

Weitere Seiten zum Thema

Hier einige weitere Seiten zu quadratischen Gleichungen:

Index Rechenregeln für Quadratische Gleichungen Online-Rechner Quadratische Gleichung Grafische Darstellung von Parabeln