Kalkulator online trygonometria

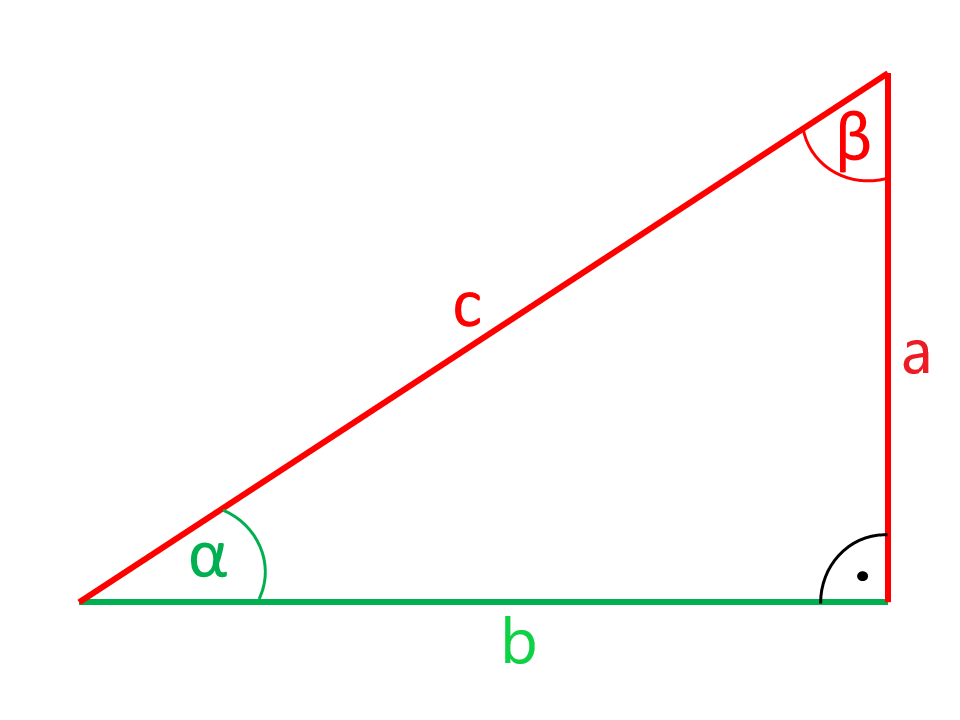
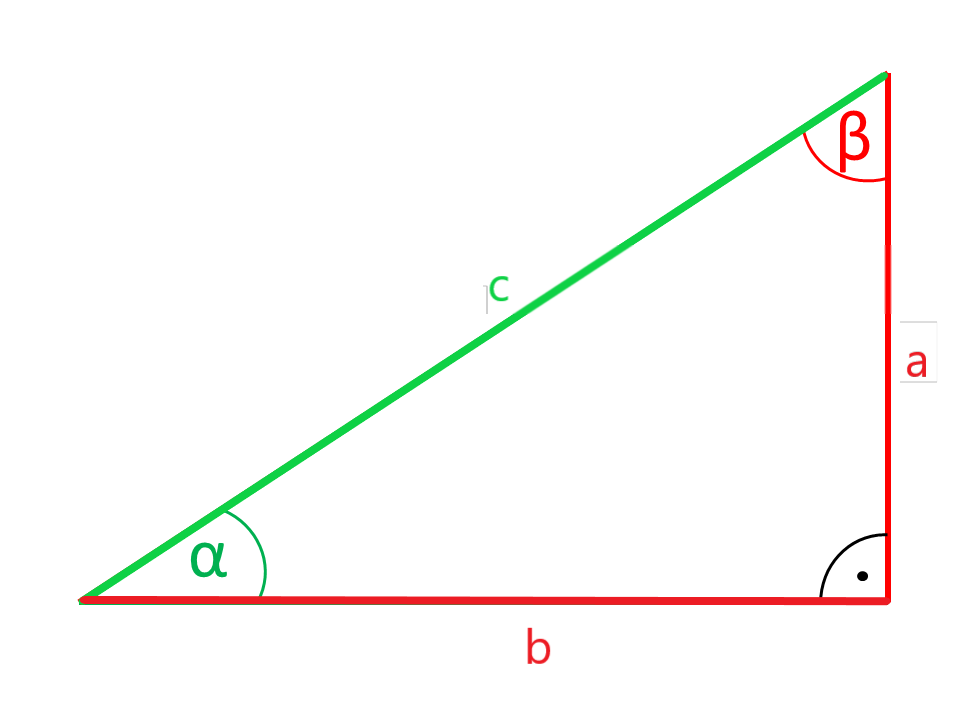
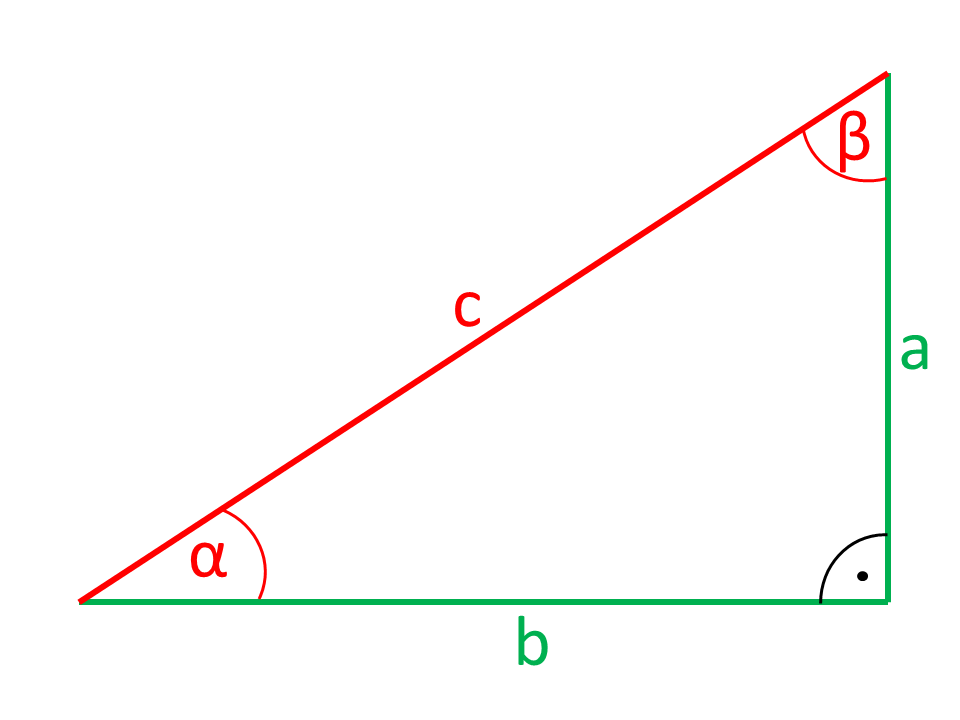
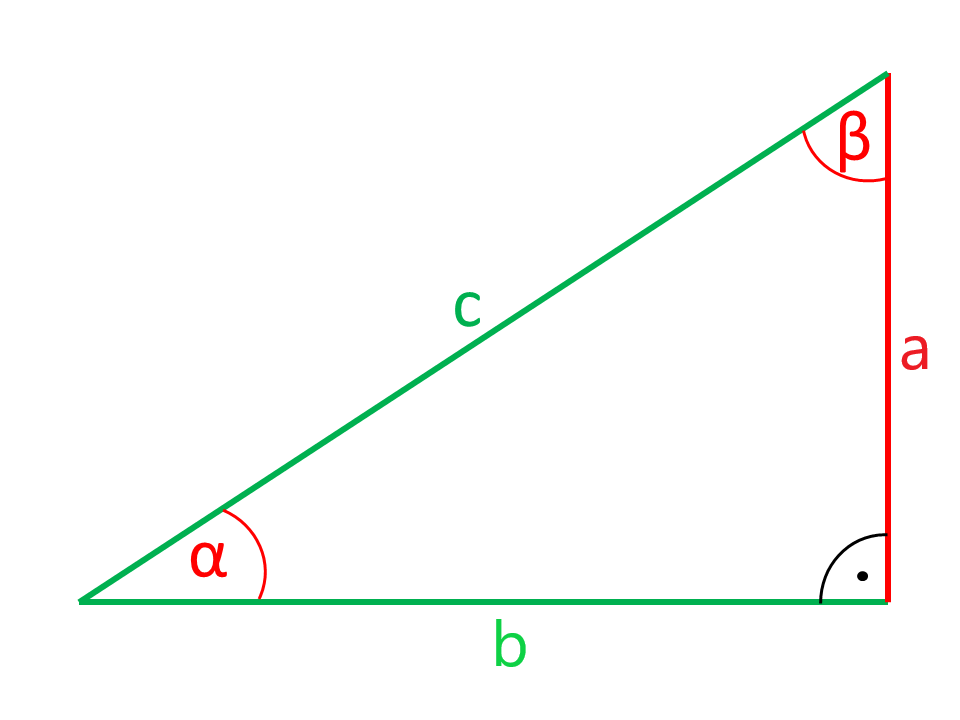
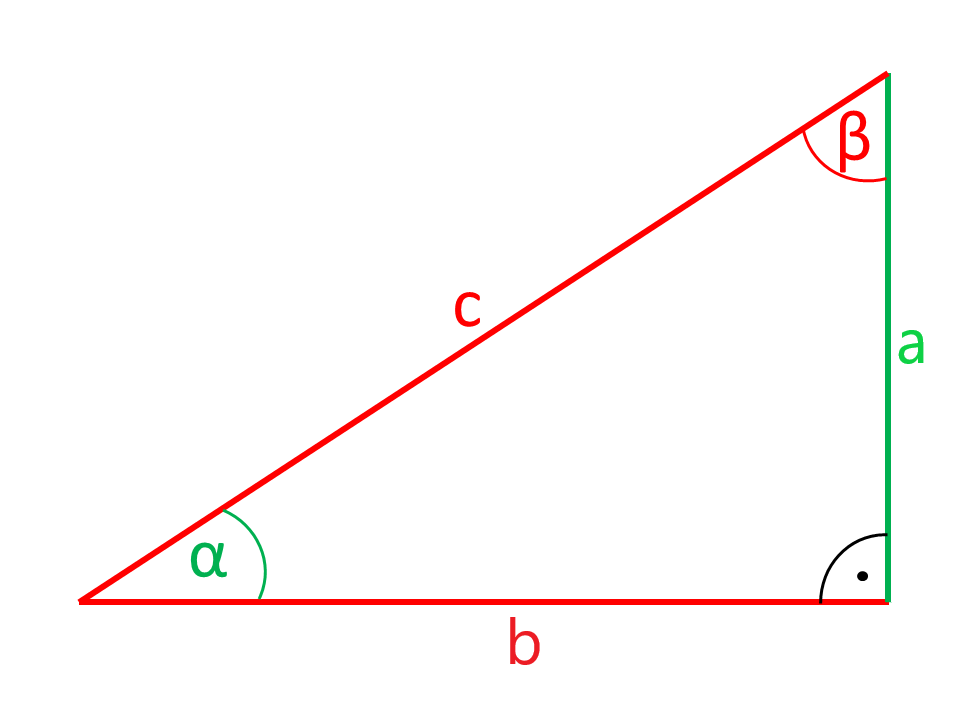
Kalkulator do obliczeń trójkątów na trójkącie prostokątnym

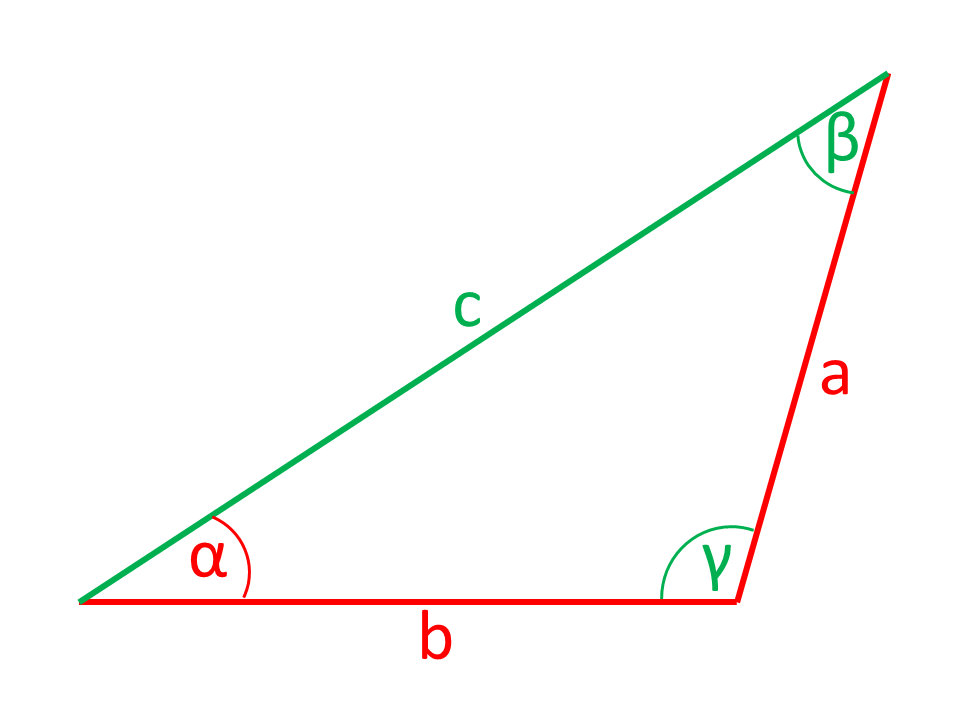
Strony lub Kątownik narysowane na czerwono na rysunkach są obliczane ze stron i Kątowników narysowanych na zielono.

Podane: Kątownik i przeciwległe przyprostokątnymi

α w stopniach =

a =

Podane: Kątownik i przyległy przyprostokątnymi

α w stopniach =

b =

Podane: Kątownik i przeciwprostokątną

α w stopniach =

c =

Podane: przyprostokątnymi

a =

b =

Podane: przyprostokątnymi i przeciwprostokątną

b =

c =

Kalkulator do obliczeń trójkątów na trójkącie ogólnym (skośnym)

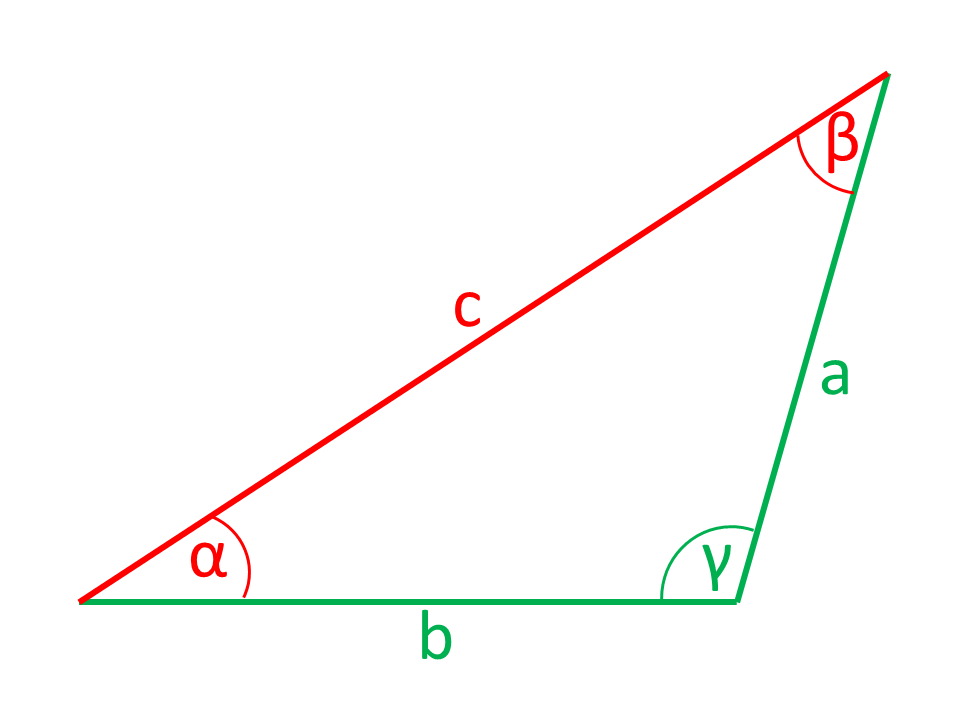
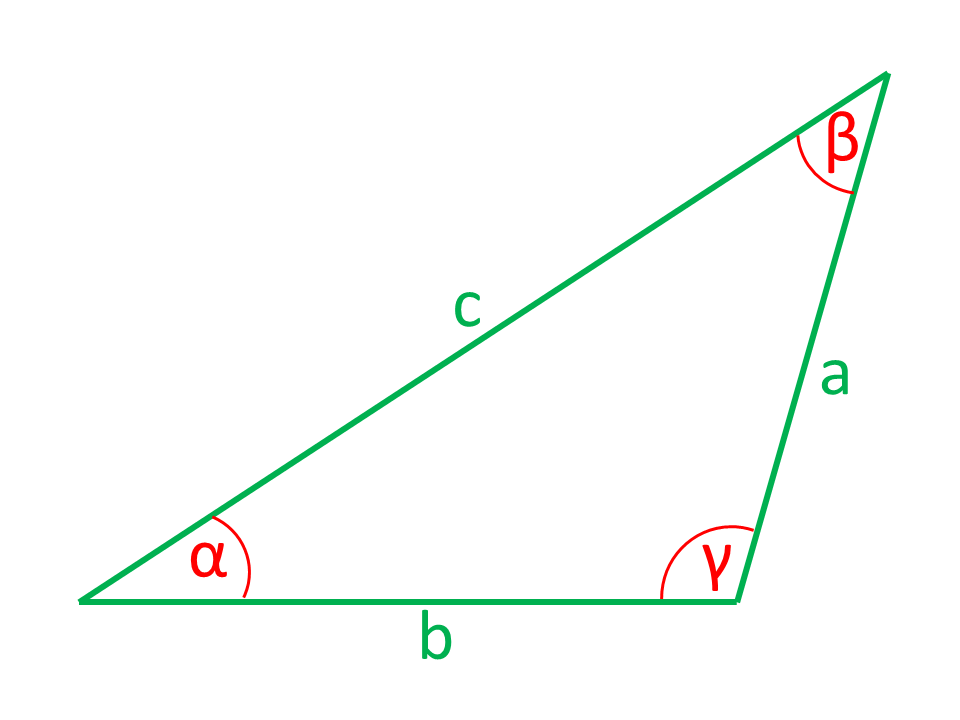
Strony lub Kątownik narysowane na czerwono na rysunkach są obliczane ze stron i Kątowników narysowanych na zielono.

Podane: Dwa Strony i Kątownik

γ w stopniach =

a =

b =

Dane: Dwa kąty i jeden bok

γ w stopniach =

β w stopniach =

c =

Podane: Trzy Strony

a =

b =

c =

Przykłady zastosowania obliczeń trygonometrycznych

Poniżej przedstawiono kilka przykładów ilustrujących zastosowanie wzorów trygonometrycznych.

Przykład: Obliczenie wysokości wieży

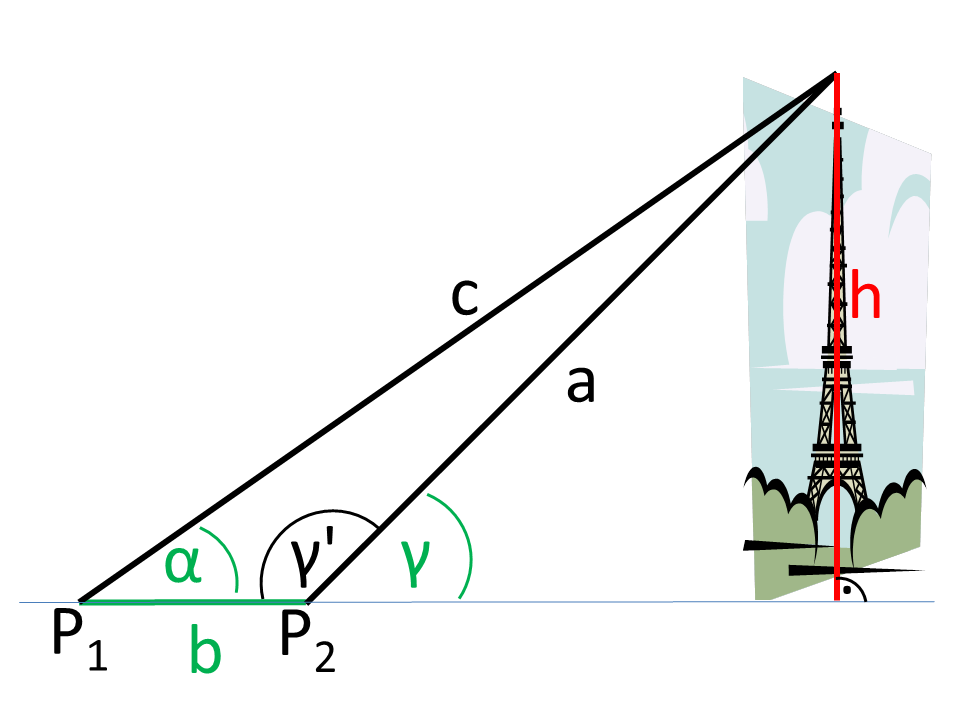
Przykład pokazuje, jak można określić wysokość, nawet gdy bezpośredni dostęp nie jest możliwy.

Na rysunku widać, że z dwóch stanowisk (P₁, P₂) wyznaczono kąty widzenia (&alfa;, γ) oraz odległość b stanowisk (kolor zielony na rysunku).

Z punktów P₁, P₂ i wierzchołka wieży utworzono trójkąt. Z tego ogólnego trójkąta znane są kąt &alfa; i bok b. Kąt γ' można obliczyć w następujący sposób:

$\mathrm{\gamma \text{'}}=180-\mathrm{\gamma }$

Brakujący kąt β można wyznaczyć, bo suma kątów w trójkącie wynosi 180°.

$\beta =180-\mathrm{\alpha }-\mathrm{\gamma \text{'}}=\mathrm{\gamma }-\mathrm{\alpha }$

W kolejnym kroku do obliczenia boku a wykorzystuje się twierdzenie sinusów. Bok a jest wspólnym bokiem trójkąta ogólnego i trójkąta prostokątnego utworzonego przez a oraz wysokość wieży i linię podstawy.

$a=\sin \left(\alpha \right)\frac{b}{\sin \left(\beta \right)}=b\frac{\sin \left(\alpha \right)}{\sin \left(\gamma -\alpha \right)}$

W trójkącie prostokątnym a jest hipotezą, a h przeciwległą katetą kąta γ. Szukaną przez nas wysokość h możemy zatem obliczyć za pomocą funkcji kąta.

$h=a\sin \left(\gamma \right)=b\frac{\sin \left(\alpha \right)\sin \left(\gamma \right)}{\sin \left(\gamma -\alpha \right)}$

Alternatywnie wysokość wieży można również obliczyć stosując dwa równania dla trójkątów prostokątnych. Pierwszy trójkąt wynika z P₁ i punktu bazowego wieży oraz wierzchołka wieży. Drugi trójkąt jest analogiczny, ale oparty na P₂.

Dotyczy:

$\tan \gamma =\frac{h}{x}$

i

$\tan \alpha =\frac{h}{b+x}$

o nieznanej odległości x od punktu P₂ do punktu bazowego wieży.

Przekształcenie równań daje w każdym przypadku:

$x=\frac{h}{\tan \gamma }$

i

$x=\frac{h-b\tan \alpha }{\tan \alpha }$

Równanie równań i rozwiązanie dla h daje rozwiązanie:

$h=b\frac{\tan \alpha \tan \gamma }{\tan \gamma -\tan \alpha }$

Że oba rozwiązania dla h są równoważne, można łatwo udowodnić przez

$\tan \left(\alpha \right)=\frac{\sin \left(\alpha \right)}{\cos \left(\alpha \right)}$

i

$\tan \left(\gamma \right)=\frac{\sin \left(\gamma \right)}{\cos \left(\gamma \right)}$

zastępuje.

$h=b\frac{\tan \alpha \tan \gamma }{\tan \gamma -\tan \alpha }=b\frac{\sin \alpha \sin \gamma }{\sin \gamma \cos \alpha -\sin \alpha \cos \gamma }$

Z twierdzenia o dodawaniu

$\sin \left(x\pm y\right)=\sin \left(x\right)\cos \left(y\right)\pm \cos \left(x\right)\sin \left(y\right)$

skutkuje powyższym rozwiązaniem.

Dlatego też

$h=b\frac{\tan \alpha \tan \gamma }{\tan \gamma -\tan \alpha }=b\frac{\sin \left(\alpha \right)\sin \left(\gamma \right)}{\sin \left(\gamma -\alpha \right)}$

Przykład: Łożysko poprzeczne

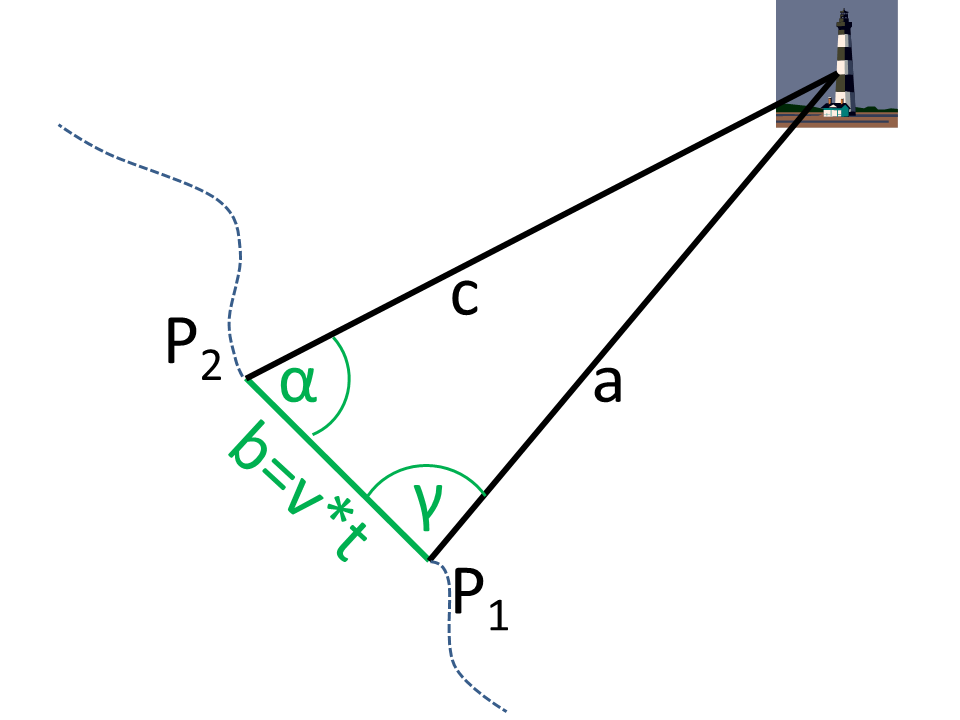
W łożysku poprzecznym punkt stały (np. latarnia morska) jest przyjmowany z dwóch pozycji. Między dwoma łożyskami (P₁, P₂) przebywa się stały kurs i stałą prędkość. Następnie na podstawie namiarów można określić odległość do punktu docelowego.

Na rysunku widać, że w dwóch miejscach (P₁, P₂) wyznaczono kąty widzenia (&alfa;, γ) względem kierunku jazdy (kolor zielony na rysunku). Długość boku b wynika z prędkości v i odległości czasowej t pomiarów.

Z punktów P₁, P₂ i punktu docelowego (latarni) powstaje trójkąt. Z tego ogólnego trójkąta znane są kąt &alfa; i bok b = v * t.

Brakujący kąt β można wyznaczyć, bo suma kątów w trójkącie wynosi 180°.

$\beta =180-\mathrm{\alpha }-\mathrm{\gamma }$

W kolejnym kroku do obliczenia boku a wykorzystuje się twierdzenie sinusów. Bok a jest odległością do punktu pomiarowego P₁.

$a=\sin \left(\alpha \right)\frac{b}{\sin \left(\beta \right)}$

Analogicznie oblicza się odległość do drugiego punktu pomiarowego.

$c=\sin \left(\gamma \right)\frac{a}{\sin \left(\alpha \right)}$

Przykład: Pomiar niedostępnego odcinka (zadanie Hansena)

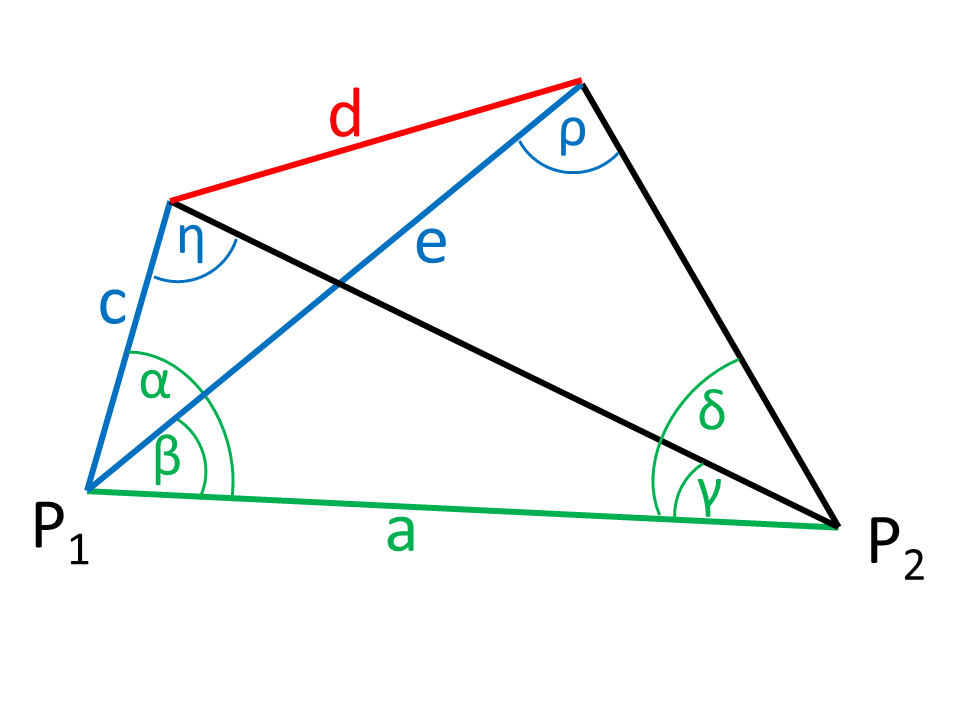
Aby zmierzyć trasę niedostępną, do początku i końca trasy dąży się z dwóch punktów (P₁, P₂).

Z rysunku wynika, że w dwóch miejscach (P₁, P₂) wyznaczono kąty widzenia (&alfa;, β, γ, δ) na początku i końcu odległości względem osi łączącej punkty (kolor zielony na rysunku). Znana jest również odległość a punktów pomiarowych. Należy wyznaczyć długość niedostępnego odcinka d (kolor czerwony na rysunku).

Na rysunku na niebiesko zaznaczono wartości pośrednie, które należy obliczyć.

Kąt η można wyznaczyć, bo suma kątów w trójkącie wynosi 180°.

$\eta =180-\mathrm{\alpha }-\mathrm{\gamma }$

W kolejnym kroku do obliczenia boku c wykorzystuje się twierdzenie sinusów.

$c=a\frac{\sin \left(\gamma \right)}{\sin \left(\eta \right)}$

Bok e również oblicza się za pomocą twierdzenia sinusów.

$e=a\frac{\sin \left(\delta \right)}{\sin \left(\rho \right)}$

Kąt ρ wynika z sumy kątów w trójkącie.

$\rho =180-\mathrm{\beta }-\mathrm{\delta }$

Twierdzenie cosinusów można teraz wykorzystać do obliczenia szukanej przez nas odległości d.

$d^2=a^2+c^2-2ac\cos \left(\alpha -\beta \right)$

Przykład: Trójkąt sił działających na wahadło

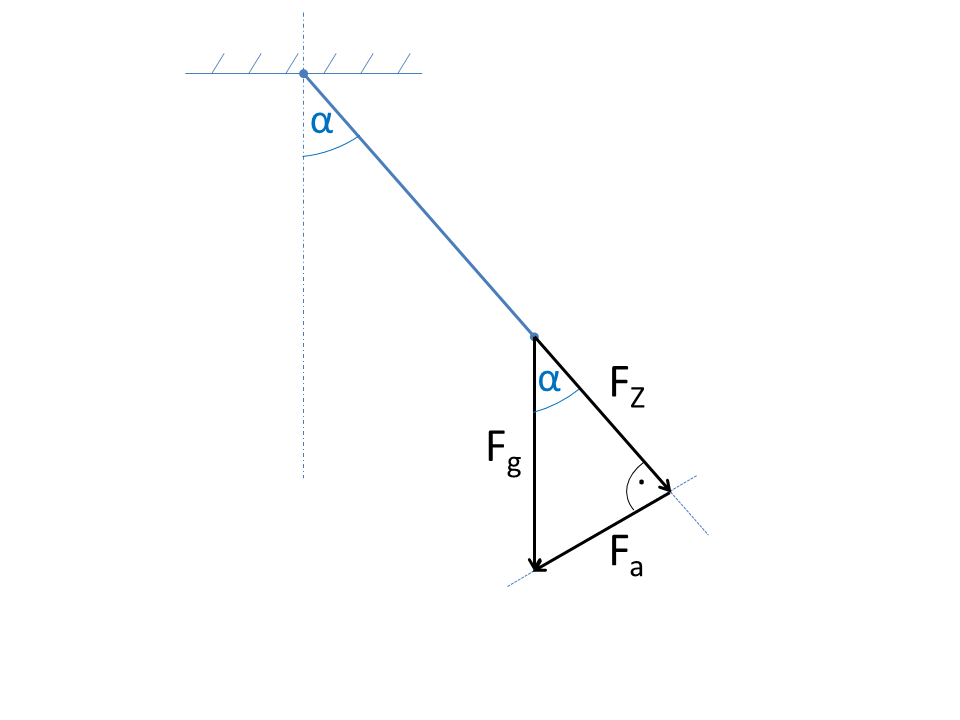
Rozkład sił na składowe ortogonalne odgrywa ważną rolę w mechanice. W tym przykładzie pokazano, jak siłę ciężaru można rozłożyć na dwie składowe za pomocą funkcji kątowych.

Na rysunku przedstawiono wahadło z nitką, na której końcu znajduje się masa. Siłę ciężaru F_g należy rozłożyć na siły cząstkowe. Siła w kierunku nici F_Z nie ma udziału w przyspieszeniu, dlatego dla równania ruchu istotna jest znajomość siły F_a.

Siły cząstkowe można określić bezpośrednio poprzez funkcje kątowe, ponieważ jest to trójkąt prostokątny.

$F_a=F_g\sin \left(\alpha \right)$

$F_Z=F_g\cos \left(\alpha \right)$

Trygonometria ogólnie

Podstawowym zadaniem trygonometrii jest obliczanie innych wielkości danego trójkąta (długości boków, wielkości kątów, długości trójkątów­poprzecznych itp.) z trzech wielkości tego trójkąta. Jako pomoc stosuje się funkcje trygonometryczne sin (sin), cosinus (cos), tangens (tan), cotangens (cot). Prekursorzy trygonometrii istnieli już w starożytnej matematyce greckiej. Arystarchus z Samos wykorzystał własności trójkątów prostokątnych do obliczania odległości­między Ziemią a Słońcem lub Księżycem.

Trójkąt prosty

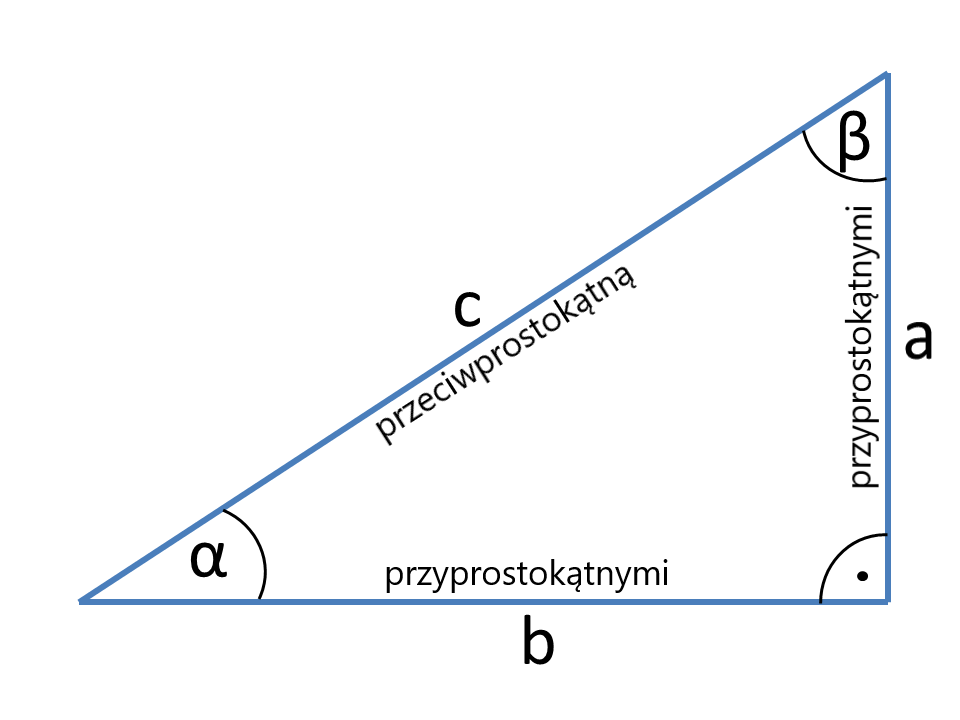
Definicje

Boki a i b trójkąta prostego zamykające kąt prosty to przyprostokątnymi. Bok c leżący naprzeciwko kąta prostego to przeciwprostokątną. Jeśli spojrzymy na kąt &alfa; to bok a jest przyprostokątnymi przyległą, a b przyprostokątnymi przeciwległą.

Funkcje kątowe

$\sin \left(\alpha \right)=\cos \left(\beta \right)=\frac{a}{c}$

$\cos \left(\alpha \right)=\sin \left(\beta \right)=\frac{b}{c}$

$\tan \left(\alpha \right)=\cot \left(\beta \right)=\frac{a}{b}$

Stopień / Radiant

Kąt można określić w gradach (deg) lub radianach (rad). Pełny okrąg w gradach to 360 stopni, w radianach to 2π. W związku z tym obowiązują następujące przeliczenia.

$\text{Kątownik (rad)}=\frac{\pi }{180}\text{Angle (deg)}$

$\text{Kątownik (deg)}=\frac{180}{\pi }\text{Angle (rad)}$

Suma kątów

Suma kątów w trójkącie wynosi 180°. Zatem dla kątów w trójkącie prostokątnym obowiązuje następująca zależność.

$90=\alpha +\beta$

Trójkąt ogólny (skośny)

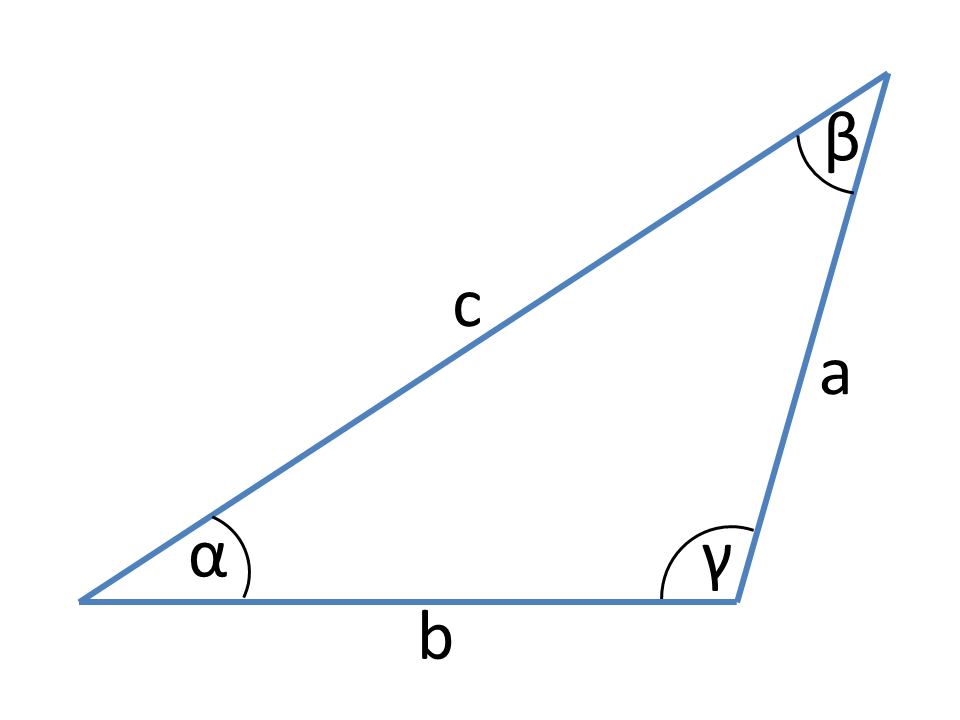
Definicje

Istotne dla obliczeń w trójkącie ogólnym są twierdzenia o cosinusie i sinusie oraz związki funkcji kątowych.

Zestaw sinusoidalny

$\frac{a}{\sin \left(\alpha \right)}=\frac{b}{\sin \left(\beta \right)}=\frac{c}{\sin \left(\gamma \right)}$

Twierdzenie cosinusów

$a^2=b^2+c^2-2bc\cos \left(\alpha \right)$

$b^2=a^2+c^2-2ac\cos \left(\beta \right)$

$c^2=a^2+b^2-2ab\cos \left(\gamma \right)$

Zestaw projekcyjny

$c=a\cdot \cos \left(\beta \right)+b\cdot \cos \left(\alpha \right)$

Wzór na styczną

$\tan \left(\gamma \right)$$=\frac{c\cdot \sin \left(\alpha \right)}{b-c\cdot \cos \left(\alpha \right)}$$=\frac{c\cdot \sin \left(\beta \right)}{a-c\cdot \cos \left(\beta \right)}$

Suma kątów

Suma kątów w trójkącie jest równa 180°.

$180=\alpha +\beta +\gamma$

Promień obwodu r

$r=\frac{s}{4\cdot \cos \left(\frac{\alpha }{2}\right)\cdot \cos \left(\frac{\beta }{2}\right)\cdot \cos \left(\frac{\gamma }{2}\right)}$

z

$s=\frac{1}{2}\left(a+b+c\right)$

Promień wewnątrz okręgu ρ

$\rho =\sqrt{\frac{\left(s-a\right)\left(s-b\right)\left(s-c\right)}{s}}$

Wysokość h_c do c

$h_c=a\cdot \sin \left(\beta \right)=b\cdot \sin \left(\alpha \right)$

Obszar A

$A=\frac{1}{2}a\cdot b\cdot \sin \left(\gamma \right)$

Wzór na obszar Herona

$A=\rho s=\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}$

Własności funkcji trygonometrycznych

Wzór na redukcję (w stopniach)

$\sin \left(\mathrm{90°}+x\right)=\cos \left(x\right)$

$\cos \left(\mathrm{90°}+x\right)=-\sin \left(x\right)$

$\tan \left(\mathrm{90°}+x\right)=-\cot \left(x\right)$

$\cot \left(\mathrm{90°}+x\right)=-\tan \left(x\right)$

$\sin \left(\mathrm{180°}+x\right)=-\sin \left(x\right)$

$\cos \left(\mathrm{180°}+x\right)=-\cos \left(x\right)$

$\tan \left(\mathrm{180°}+x\right)=\tan \left(x\right)$

$\cot \left(\mathrm{180°}+x\right)=\cot \left(x\right)$

Korelacja funkcji trygonometrycznych o tym samym argumencie

${\sin \left(x\right)}^2+{\cos \left(x\right)}^2=1$

$\tan \left(x\right)=\frac{\sin \left(x\right)}{\cos \left(x\right)}$

Twierdzenia o dodawaniu funkcji trygonometrycznych

$\sin \left(x\pm y\right)=\sin \left(x\right)\cos \left(y\right)\pm \cos \left(x\right)\sin \left(y\right)$

$\cos \left(x\pm y\right)=\cos \left(x\right)\cos \left(y\right)\mp \sin \left(x\right)\sin \left(y\right)$

$\tan \left(x\pm y\right)=\frac{\tan \left(x\right)\pm \tan \left(y\right)}{1\mp \tan \left(x\right)\tan \left(y\right)}$

Więcej stron na ten temat

Oto kilka kolejnych stron:

Treść ćwiczenia z matematyki

Matryca

Iloczyn wektorowy macierzy

Transformata Fouriera

Kalkulator Transformata Fouriera