Online interaktive Ellipse

Interaktiver grafischer Ellipsenrechner

Durch schieben der Punkt oder mittels Eingabe der Koordinaten in den numerischen Eingabefeldern kann die Ellipse definiert werden. Die Brennpunkte F₁, F₂ und der Peripheriepunkt P erlauben die Bestimmung der Ellipse. Das Zentrum der Ellipse ist durch den Mittelpunkt C gegeben. Die aktuell berechneten Ellipsenwerte werden in der folgenden Tabelle angezeigt.

⃢

↹#.000

🔍↔

🔍↕

Ellipse:

Exzentrizität e=

Umfang U≈

Fläche F=

Halbachsen:

C V₁=

C V₂=

Summe=

Brennpunktlinien:

p F₁=

p F₂=

Summe=

Brennpunktabstand:

F₁F₂=

α=

Tangentensteigung in p=

Punkte (x, y)

F₁ =

F₂ =

P =

Wertebereich der Achsen

x-min=

x-max=

y-min=

y-max=

Ellipse:

F₁, F₂, P:

Halbachse C V₁, C V₂:

C, V₁, V₂:

Brennlinien p F₁, p F₂:

Tangente:

Normale:

Eigenschaften der Ellipse

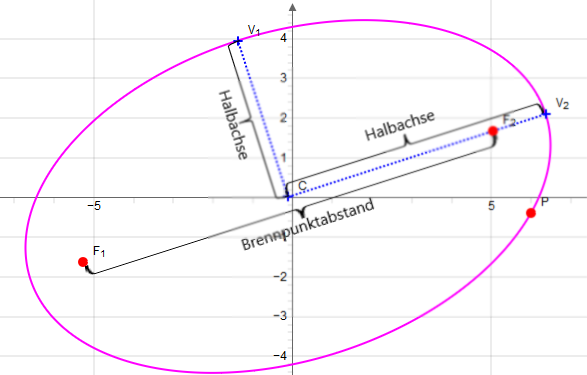
Die Ellipse ist die Menge aller geometrischen Orte für die die Summe der Abstände von zwei festen Punkten konstant ist.

Die Ellipse ist in kartesischen Koordinaten gegeben durch:

$\frac{{(x - m_{x})}^{2}}{a^{2}} + \frac{{(y - m_{y})}^{2}}{b^{2}} = 1$

mit dem Ellipsenmittelpunkt M bei m_x und m_y.

In Parameterdarstellung ist die Ellipse gegeben wie folgt

$(\begin{matrix} m_{x} + a \cos t \\ m_{y} + b \sin t \end{matrix})$

Umfang der Ellipse

Mit den Halbachsen a = C V₁ und b = C V₂ ist der Umfang der Ellipse gegeben durch:

$U = π (a + b) (1 + \sum_{n = 0}^{\infty} \frac{(\begin{matrix} 2n \\ n \end{matrix})}{(n + 1) 2^{2 n + 1}} 2^{2 n + 2})$

$= π (a + b) (1 + \frac{λ^{2}}{4} + \frac{λ^{4}}{64} + ...)$

mit

$λ = \frac{(a - b)}{(a + b)}$

Näherungsformel für den Ellipsenumfang nach Ramanujan:

$U \approx π (a + b) (1 + \frac{3 λ^{2}}{10 + \sqrt{4 - 3 λ^{2}}})$

Fläche der Ellipse

Mit den Halbachsen a und b ist die Fläche der Ellipse gegeben durch:

$F = π a b$

Brennpunktabstand

Mit der größeren Halbachse a ist der Abstand der Brennpunkte der Ellipse gegeben durch:

$d = 2 \sqrt{a^{2} - b^{2}}$

Exzentrizität

Mit der größeren Halbachse a ist Exzentrizität der Ellipse gegeben durch:

$e = \frac{d}{2 a}$

Tangente

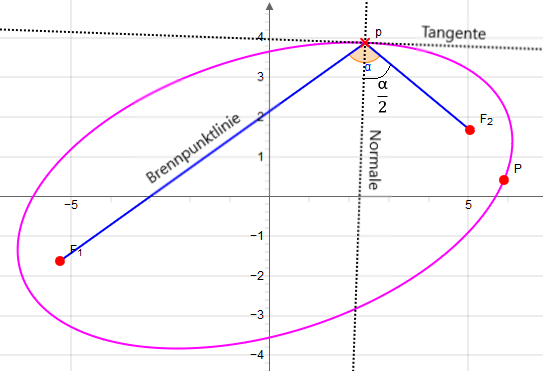
Die Normale an die Tangente der Ellipse halbiert den Winkel den die Brennpunktstrahlen an diesem Punkt bilden.

Druck und speicherbares Bild

Drucken oder Speichern der Abbildung mit Anwahl über die rechte Maustaste.

Weitere Seiten zum Thema

Hier ist eine Liste weiterer Seiten:

Index Dreieck Rechteck Parallelogramm Kreis