Online interaktiver Kreis

Kreisrechner mit Segment (Kreisabschnitt)- und Sektorberechnung

Die Punkte A und B definieren den Kreis und können numerisch oder grafisch verändert werden. A legt den Mittelpunkt fest und B den Radius. C bestimmt den Sektor und das Segment (auch Kreisabschnitt). Für den Kreis werden die Kreisdaten Kreisradius, Kreisfläche und Kreisumfang berechnet. Für das Sektorelement die Sekantenlänge, der Öffnungswinkel und die Sektorfläche. Für das Segment die Bogenlänge des Kreissegments, die Fläche des Kreissegments und die Höhe des Segments. Mit dem Kreuz auf dem Radius kann der Ring verändert werden. Für den Ring werden die Fläche und der Sektorausschnitt des Rings berechnet. Die Checkboxen ermöglichen das Ein- und Ausschalten der grafischen Elemente.

⃢

↹#.000

🔍↔

🔍↕

Kreis:

Radius

Umfang

Fläche

Sektor:

Sekantenlänge

Fläche

Winkel

Segment:

Bogenlänge

Fläche

Höhe

Ring:

Breite

Fläche

Punkte (x, y)

A =

B =

C =

Wertebereich der Achsen

x-min=

x-max=

y-min=

y-max=

Kreis:

Sekante:

Sektor:

Segment:

Höhe h_a

Punkte:

Ring:

Eigenschaften des Kreises

Kreisradius:

Der Radius r ist der Abstand vom Kreismittelpunkt zur Kreisperipherie. Ein Kreis ist definiert durch die Menge aller Punkte die den Abstand r zu einem Punkt haben.

Kreisdurchmesser:

Der Kreisdurchmesser d ist die Gerade die zwei verschiedene Punkte der Kreisperipherie verbindet und durch den Kreismittelpunkt geht.

$d = 2 r$

Kreisumfang:

$U = 2 π r = π d$

Kreisfläche:

$F = π r^{2}$

Sekante (Sehne) im Kreis

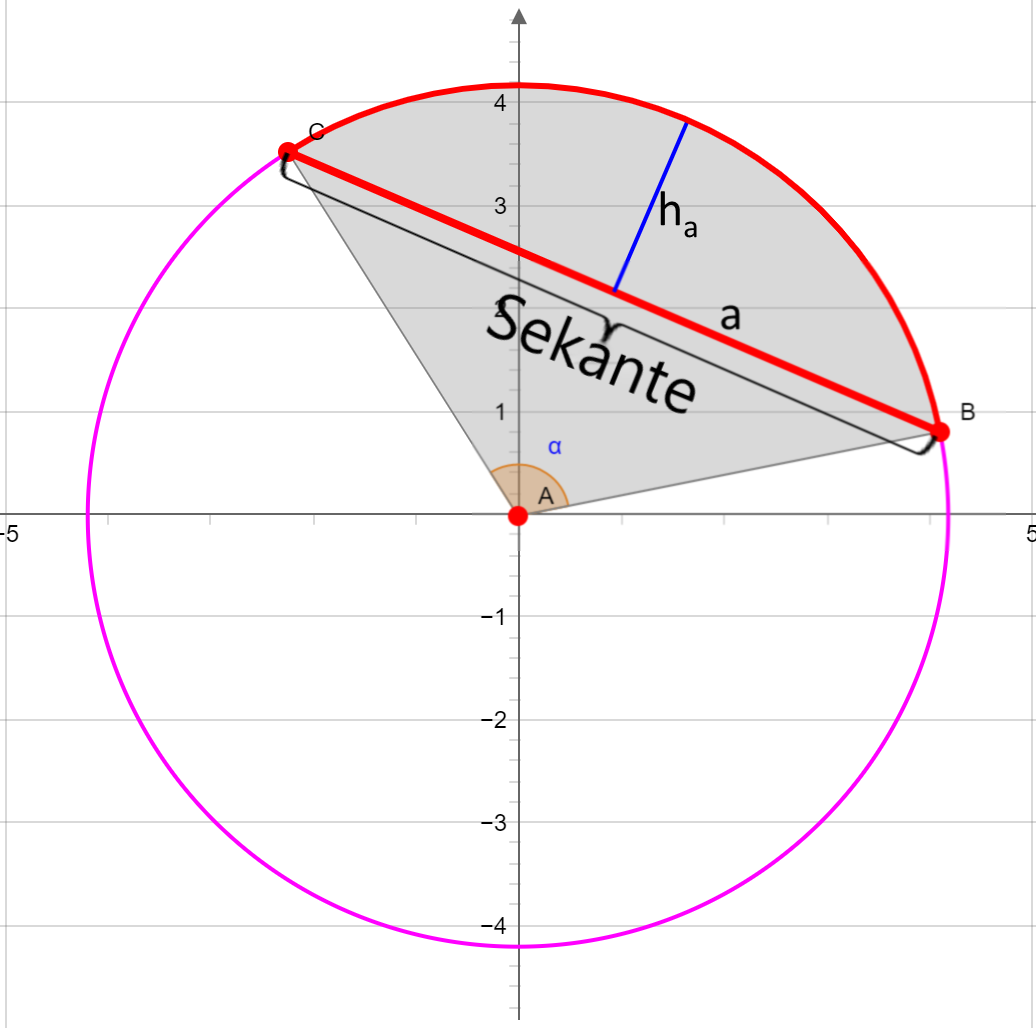
Die Sekante oder auch Sehne verbindet zwei Punkte (B und C) der Kreisperipherie. Die Länge der Sekante a ist:

$a = 2 r \sin (\frac{α}{2}) = 2 \sqrt{2 h_{a} r - {h_{a}}^{2}}$

mit dem Öffnungswinkel α des Sektors und der Höhe h_a des Kreissegments.

Bogenlänge

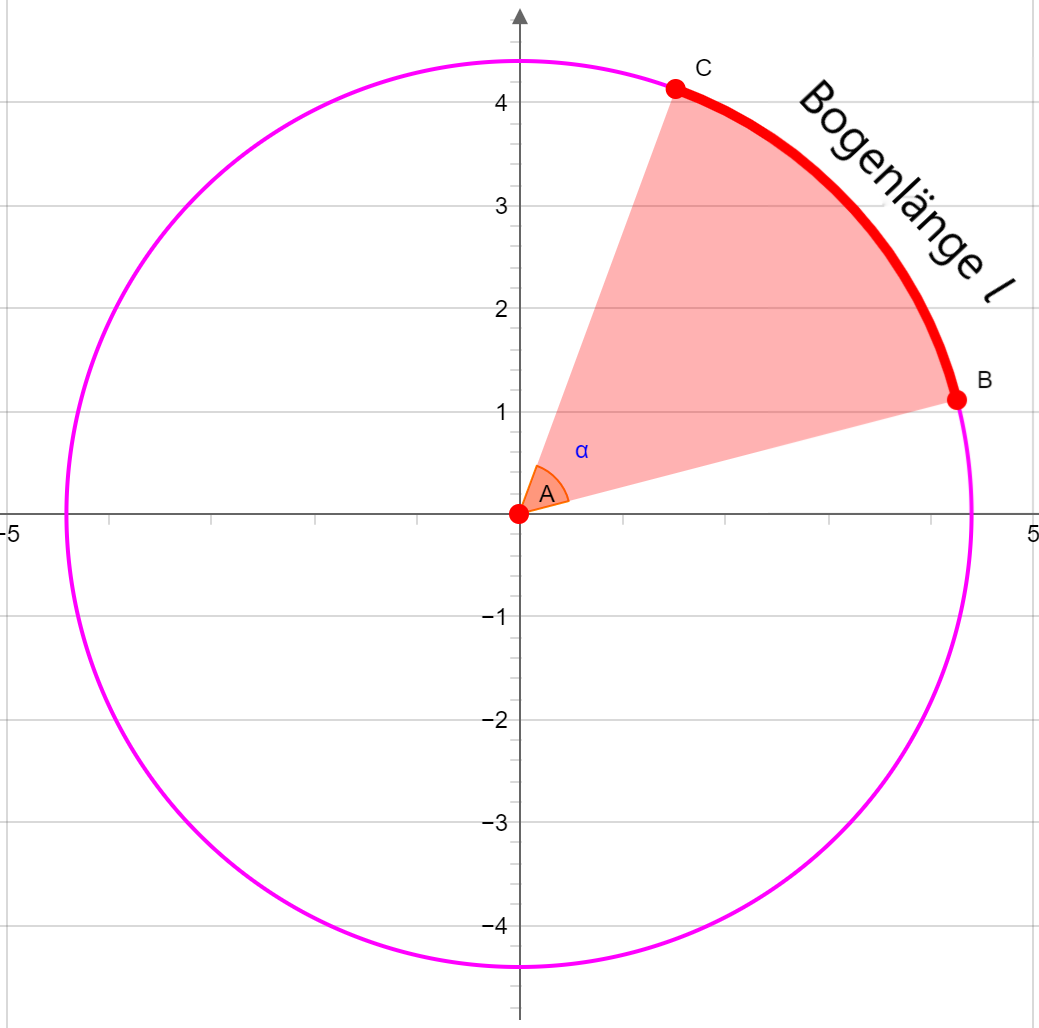
Die Bogenlänge l des Kreissegments (Kreisbogen zwischen B und C) mit dem Öffnungswinkel α des Sektors in Grad ist:

$l = 2 π r \frac{α}{360°}$

Mit dem Winkel in Radiant gilt:

$l = 2 π r \frac{α}{2 π}$

Fläche des Sektors

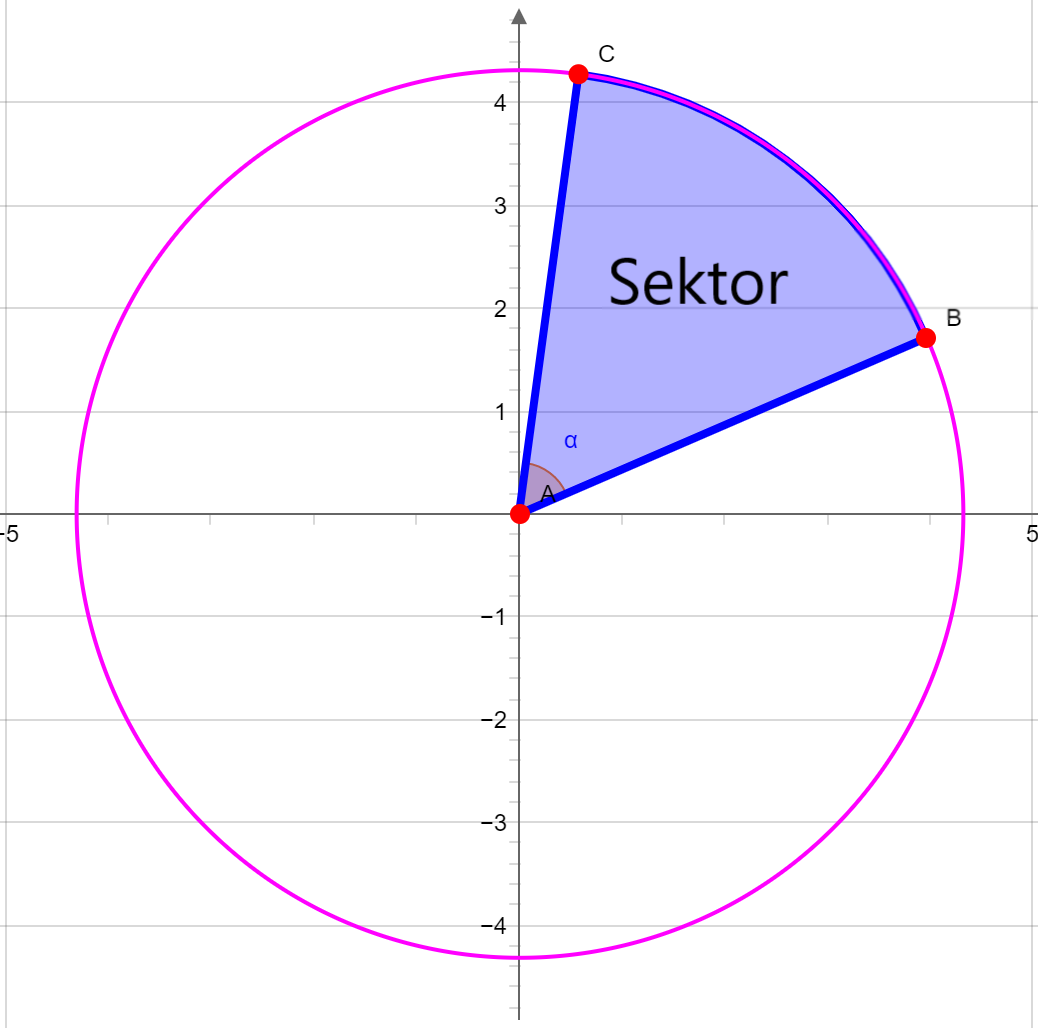
Die farbige Fläche zeigt die Fläche des Kreissektors. Die Fläche S des Kreissektors mit dem Öffnungswinkel α des Sektors in Grad ist:

$S = π r^{2} \frac{α}{360°}$

Mit dem Winkel in Radiant gilt:

$S = π r^{2} \frac{α}{2 π}$

Kreissegment (Kreisabschnitt)

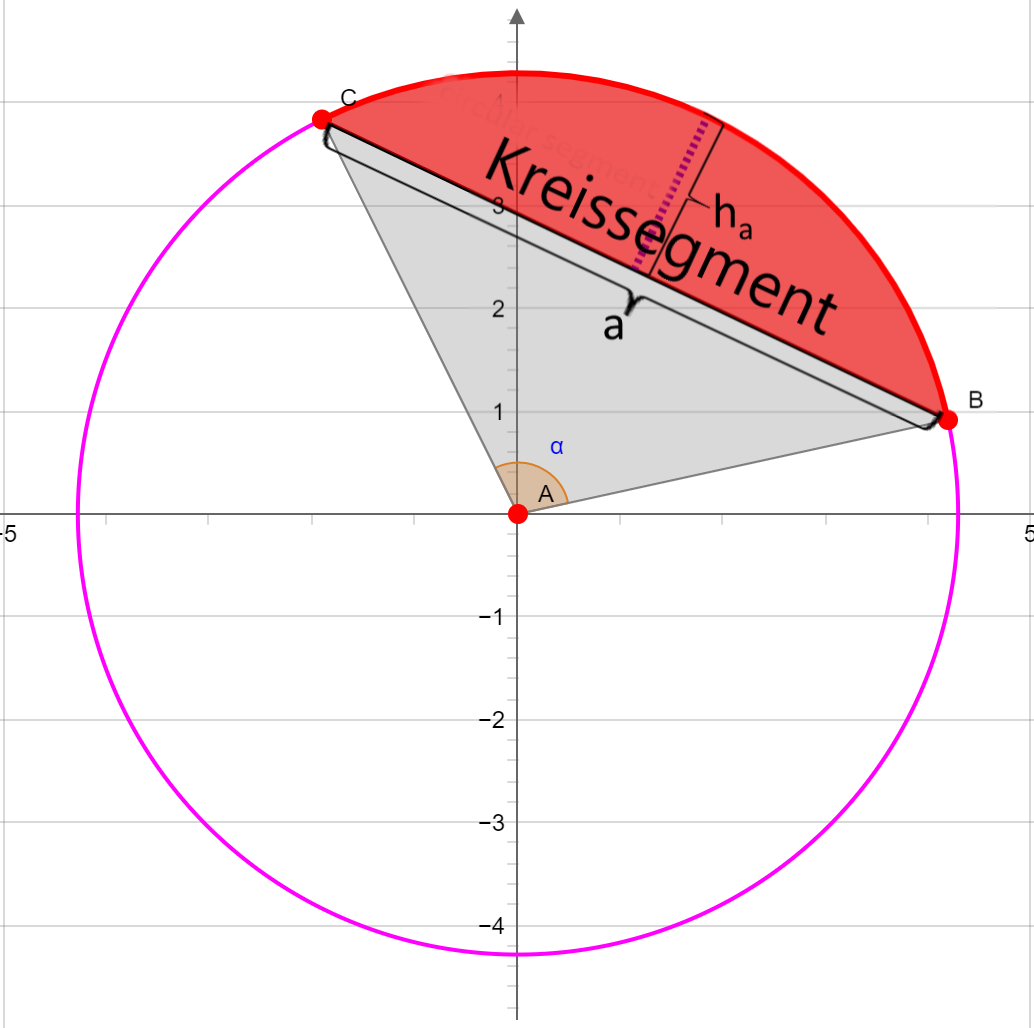
Fläche des Kreissegments:

Das Kreissegment oder Kreisabschnitt ist die Fläche zwischen Sekante (Sehne) und dem zugehörigen Kreisumfang. Die Fläche S_a des Kreissegments mit α in Radiant ist:

$S_{a} = \frac{r^{2}}{2} (α - \sin α)$

Höhe des Kreissegments:

Die Höhe h_a des Kreissegments mit der Länge der Sehne a ist:

$h_{a} = r - \sqrt{r^{2} - \frac{a^{2}}{4}}$

Kreisring

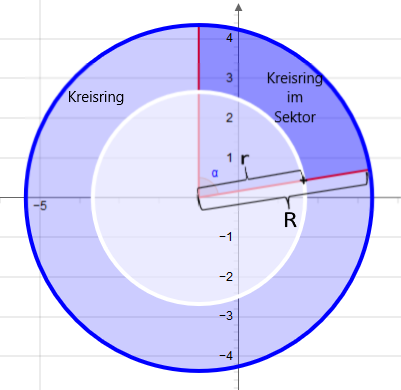
Fläche des Kreisrings:

Der Kreisring ist die Fläche zwischen dem inneren Kreis und dem äußeren Kreis. Beide Kreise haben denselben Mittelpunkt und unterscheiden sich in den Radien R und r. Die Fläche F_R des Kreisrings ist:

$F_{R} = π (R^{2} - r^{2})$

Fläche des Kreisrings im Sektor:

Die Kreisringfläche die aus einem Kreisring durch einen Sektor mit dem Öffnungswinkel α in Radiant begrenzt wird ist:

$S_{R} = \frac{α π}{2} (R^{2} - r^{2})$

Druck und speicherbares Bild

Drucken oder Speichern der Abbildung mit Anwahl über die rechte Maustaste.

Weitere Seiten zum Thema

Hier ist eine Liste weiterer Seiten:

Index Dreieck Rechteck Parallelogramm Ellipse