Logistisches Wachstum

Das Modell des exponentiellen Wachstums wird beim logistischen Wachstum um eine begrenzte Ressource erweitert. Die Lösung der Dgl beschreibt eine S-förmige Kurve, eine Sigmoide. In der Mitte der Entwicklung wächst die Population am schnellsten, bis sie durch die begrenzten Ressourcen gebremst wird.

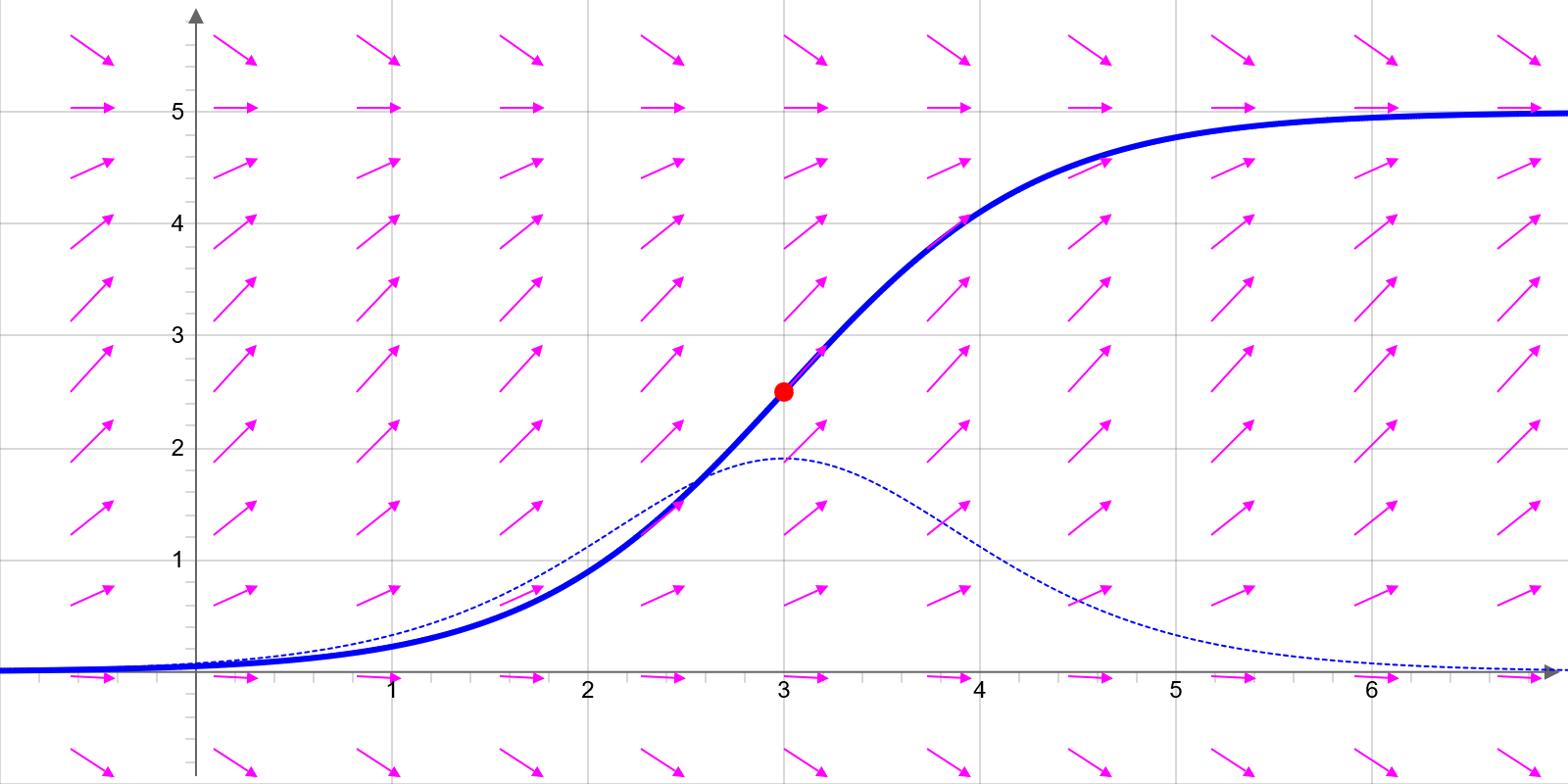
Abbildung: Die Abbildung zeigt eine logistische Wachstumskurve und ihre Ableitung als gepunktete Kurve. Das maximale Wachstum ist durch den roten Punkt gekennzeichnet. Die Vektoren zeigen das Richtungsfeld des Wachstumsmodells.

Gleichung des logistischen Wachstums

Differentialgleichung des logistischen Wachstums:

$y' (t) = k y (G - y)$

$G : Maximaler Wachstumswert$ $k : Logistische Wachstumsrate$

Mit der Wachstumsfunktion zu den Anfangsbedingungen t₀ = 0 and y₀ = y(0)

$y = \frac{G}{1 + e^{- k G t} (\frac{G}{y_{0}} - 1)}$

Mit der Wachstumsfunktion zu den allgemeinen Anfangsbedingungen t₀ and y₀ = y(t₀)

$y = \frac{G}{1 + e^{- k G (t - t_{0})} (\frac{G}{y_{0}} - 1)}$

Wendepunkt der logistischen Wachstumsfunktion:

Am Wendepunkt des logistisches Wachstums erreicht der Funktionswert die halbe Sättigungsgrenze.

$t_{W} = t_{0} + \frac{ln (\frac{G}{y_{0}} - 1)}{k G}$

$y (t_{W}) = \frac{G}{2}$

Maximale Wachstumsgeschwindigkeit:

Die maximale Wachstumsgeschwindigkeit wird im Wendepunkt erreicht.

$y' (t_{W}) = \frac{k G^{2}}{4}$

Anwendungsbeispiele

Wachstum von Populationen mit begrenzten Ressourcen
Logistische Regression
Neuronale Netzwerke
Modellierung einer Pandemie

Differentialgleichung des logistischen Wachstums

Das logistische Wachstum wird durch eine Differentialgleichungen mit den konstanten Faktoren k und G beschrieben.

$y' (t) = \frac{d y}{d t} = k y (G - y)$

Differentialgleichung des logistischen Wachstums

$k d t = \frac{1}{y (G - y)} d y$

Trennung der Variablen

$k G t + C = \ln \frac{y}{G - y}$

Integration liefert

$y = \frac{G}{1 + e^{- k G (t - t_{0})} (\frac{G}{y_{0}} - 1)}$

Auflösen und Einsetzen der Anfangsbedingung t₀, y₀ ergibt die Lösung der logistischen Differentialgleichung

Rechner für das Modell des logistischen Wachstums

⃢

↹#.000

🔍↔

🔍↕

Gitterpunkte:

Skalierung:

Funktion:

Gitter:

Screenshot der Abbildung

Drucken oder speichern Sie das Bild per Rechtsklick.

Weitere Seiten zum Thema

Hier ist eine Liste weiterer nützlicher Seiten:

Index Exponentielles Wachstum Lineare Dgl 1.Ordnung Ausgleichsgerade, Ausgleichspolynom, Fourierreihe, Potenzgesetz, Gaussfunktion. Mittelwertrechner: Arithmetisches Mittel, geometrisches Mittel, harmonisches Mittel, Median, quadratisches Mittel, kubisches Mittel. Gewichtet und ungewichtet.