Skalarprodukt (inneres Produkt) von Vektoren grafisch

Inners Produkt von zweidimensionalen (2d) Vektoren v und w

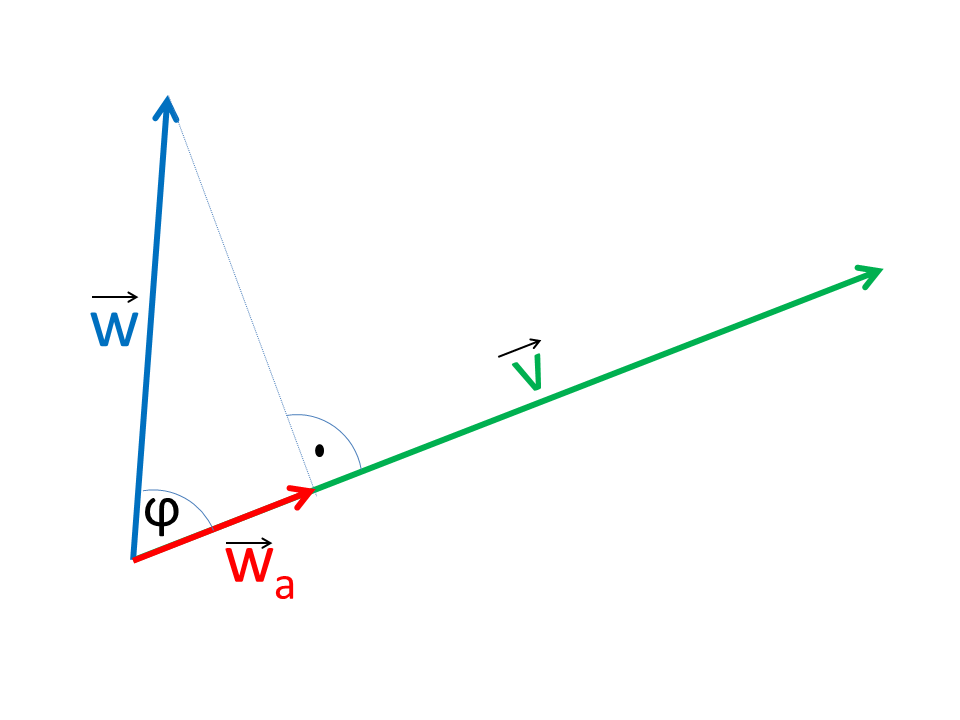
Das Skalarprodukt der Vektoren v und w wird grafisch dargestellt. Durch Ziehen der Punkte an den Vektoren können die Vektoren variiert werden. Die gepunkteten Linie zeigt die orthogonale Projektion des Vektors.

⃢

↹#.000

🔍↔

🔍↕

v_x =

v_y =

w_x =

w_y =

Skalarprodukt von Vektoren

Das Skalarprodukt ist als Produkt der Komponenten und der Summe dieser Produkte definiert. Das Skalarprodukt ist nicht von der Reihenfolge abhängig (Kommutativ). Der Name Skalarprodukt kommt daher, dass das Ergebnis ein Skalar und nicht ein Vektor ist.

$\vec{v} \cdot \vec{w} = (\begin{matrix} v_{1} \\ v_{2} \\ ⋮ \\ v_{n} \end{matrix}) \cdot (\begin{matrix} w_{1} \\ w_{2} \\ ⋮ \\ w_{n} \end{matrix})$ $= v_{1} \cdot w_{1} + v_{2} \cdot w_{2} + \dots + v_{n} \cdot w_{n}$ $= \sum_{i = 1}^{n} (v_{i} \cdot w_{i})$

Das Skalarprodukt kann geometrisch als das Produkt der Projektion des einen Vektors in die Richtung des anderen Vektors interpretiert werden. Physikalisch bedeutet das, dass das Produkt nur mit der Kompnente des Vektors gebildet wird die in Richtung des anderen Vektors wirksam ist.
Das Skalarprodukt läßt sich auch geometrisch ausdrücken. Dabei ist φ der von den Vektoren eingeschlossene Winkel.

$\vec{v} \cdot \vec{w} = | \vec{v} | | \vec{w} | \cos φ$

Für das Skalarprodukt gelten das Distributivgesetz

$\vec{u} \cdot (\vec{v} + \vec{w}) = \vec{u} \cdot \vec{v} + \vec{u} \cdot \vec{w}$

und das Kommutativgesetz

$\vec{v} \cdot \vec{w} = \vec{w} \cdot \vec{v}$

Screenshot der Abbildungen

Drucken oder speichern Sie das Bild per Rechtsklick.

Weitere Seiten zum Thema

Hier einige weitere Seiten:

Index Matrizenrechnung Determinantenrechnung Vektorrechnung Vektoraddition grafisch Vektorsubtraktion grafisch Matrix-Vektorprodukt grafisch