Vektorrechnung
Geschichte der Vektorrechnung:
Die Vektorrechnung geht zurück auf H.G. Graßmann und parallel auf Hamilton. Graßmann veröffentlichte 1844 die "Lineale Ausdehnungslehre". Als Vorläufer gelten Descartes und Möbius. Der irische Mathematiker William Rowan Hamilton (1805 - 1865) entwickelte die Theorie der Quaternionen, die als Vorläufer der Vektoren betrachtet werden. Auch der Begriff Skalar geht auf Hamilton zurück. 1888 gab der italienische Mathematiker Giuseppe Peano (1858–1932) eine axiomatische Definition eines Vektorraums, die bis auf sprachliche Nuancen unseren Axiomen eines Vektorraums entsprach.
Skalar:
Größen, die durch eine reelle Zahl angegeben werden können bezeichnet man als Skalar.In der Physik z.B. Temperatur, Masse, ...
Vektor:
Größen, die zusätzlich zu ihrem Wert die Angabe einer Richtung erfordern bezeichnet man als Vektor. In der Physik z.B. Geschwindigkeit, Feldstärke, ... Allgemein ist ein Vektor nicht auf drei Dimensionen beschränkt sondern ein n-Tupel reeller Zahlen, dass häufig als Spaltenvektor notiert wird.
Lineare Abhängigkeit:
Zwei Vektoren heißen linear Abhängig oder Kollinear, wenn der eine durch Multiplikation mit einem Skalar in den anderen überführt werden kann. Das Kreuzprodukt kollinearer Vektoren verschwindet.
Orthogonalität:
Zwei Vektoren heißen orthogonal, wenn das Skalarprodukt der beiden Vektoren verschwindet. Geometrisch stehen die Vektoren dann senkrecht aufeinander d.h. der Winkel den die Vektoren einschließen beträgt 90°.
Einheitsvektor:
Vektoren der Länge 1 werden als Einheitsvektoren bezeichnet. Jeder Vektor kann durch Normierung in den Einheitsvektor überführt werden, indem der Vektor durch seinen Betrag dividiert wird.
Rechenregeln für Vektoren
Multiplikation des Vektors mit einem Skalar
Die Multiplikation eines Vektors mit einem positiven Skalar λ ändert nur die Länge des Vektors und nicht die Richtung. Bei der Multiplikation mit einem negativen Skalar ändert sich die Richtung des Vektors in die Gegenrichtung.
Für die Multiplikation eines Vektors mit einem Skalar λ gilt das Distributivgesetz.
Addition von Vektoren
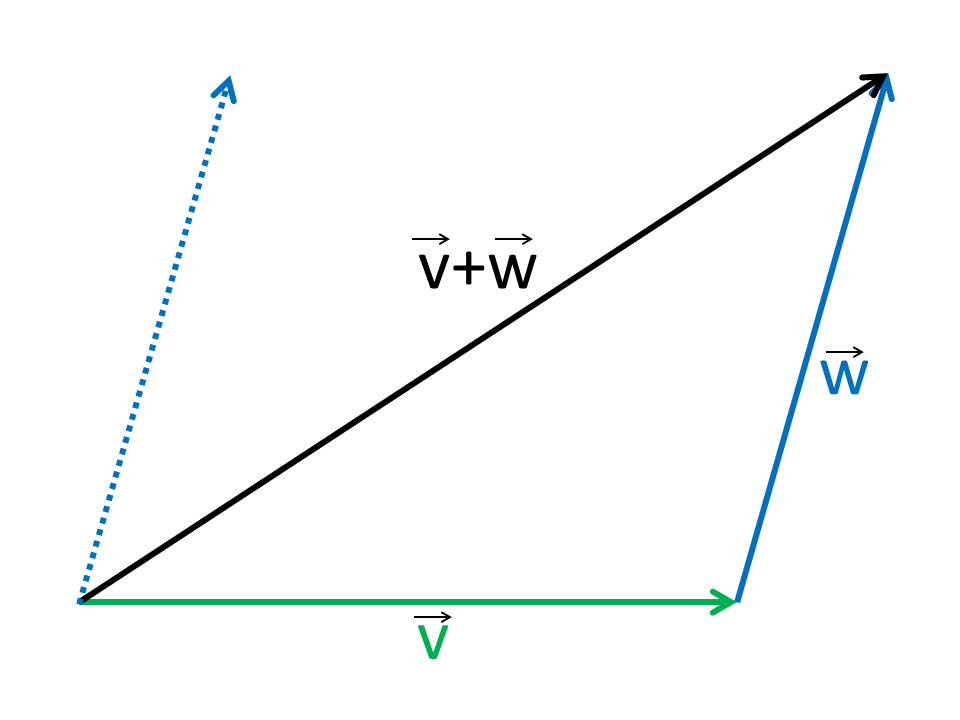
Die Addition von Vektoren erfolgt in kartesischen Koordinaten komponentenweise. Die Vektoraddition ist kommutativ und assoziativ.
Geometrisch kann der resultierende Vektor konstruiert werden, indem einer der Vektoren parallelverschoben wird in den Endpunkt des anderen Vektors. Die Verbindung von Anfangspunkt des ersten Vektors zum Endpunkt des zweiten Vektors ist der resultierende Vektor der Vektoraddition.
Subtraktion von Vektoren
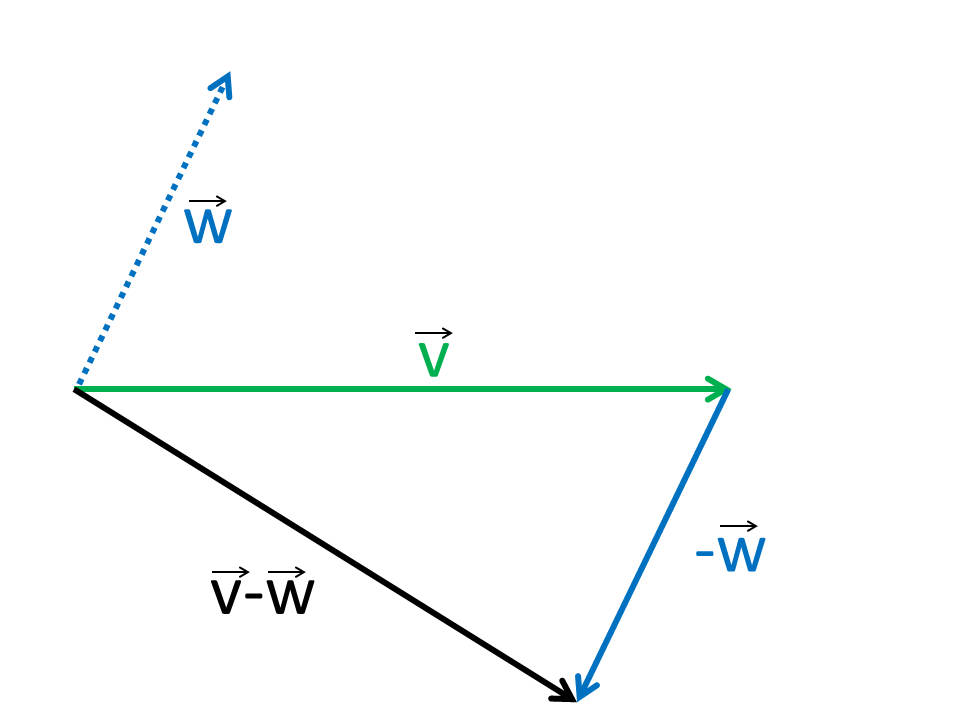
Die Subtraktion von Vektoren erfolgt wie die Addition nur indem die Komponenten subtrahiert werden.
Geometrisch ist die Konstruktion analog der Addition nur das der Vektor mit dem negativen Vorzeichen in der Richtung gespiegelt wird.
Skalarprodukt (inneres Produkt) von Vektoren
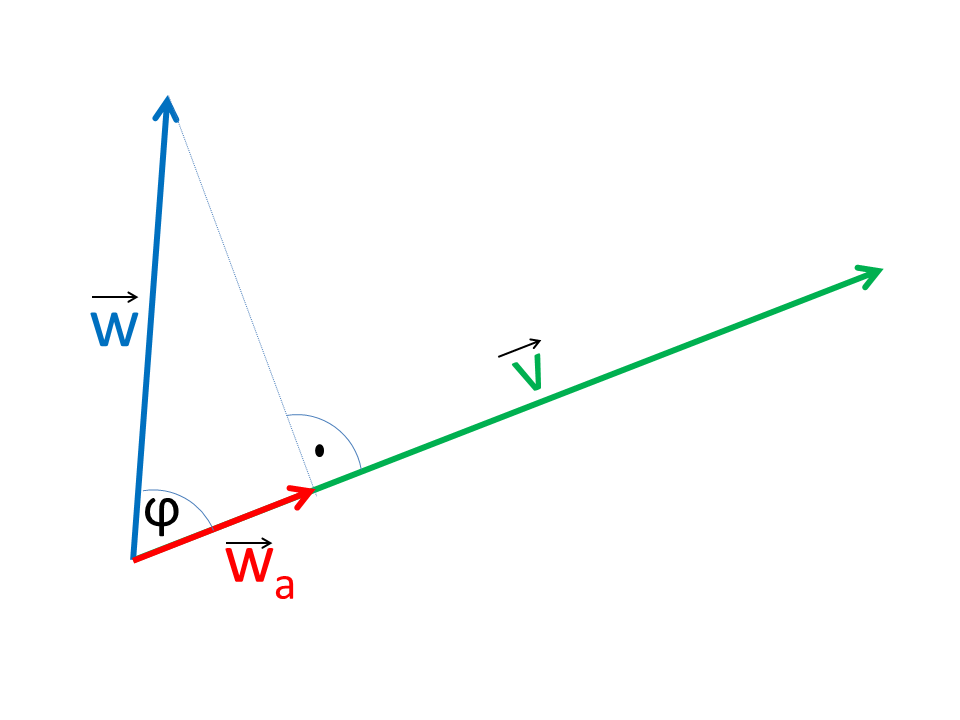
Das Skalarprodukt ist als Produkt der Komponenten und der Summe dieser Produkte definiert. Das Skalarprodukt ist nicht von der Reihenfolge abhängig (Kommutativ). Der Name Skalarprodukt kommt daher, dass das Ergebnis ein Skalar und nicht ein Vektor ist.
Das Skalarprodukt läßt sich auch geometrisch ausdrücken. Dabei ist φ der von den Vektoren eingeschlossene Winkel. Das Skalarprodukt entspricht der orthogonalen Projektion des einen Vektors in den Anderen und der Multiplikation der Beträge.
Für das Skalarprodukt gelten das Distributivgesetz
und das Kommutativgesetz
Vektorprodukt (Kreuzprodukt, äußeres Produkt) von Vektoren
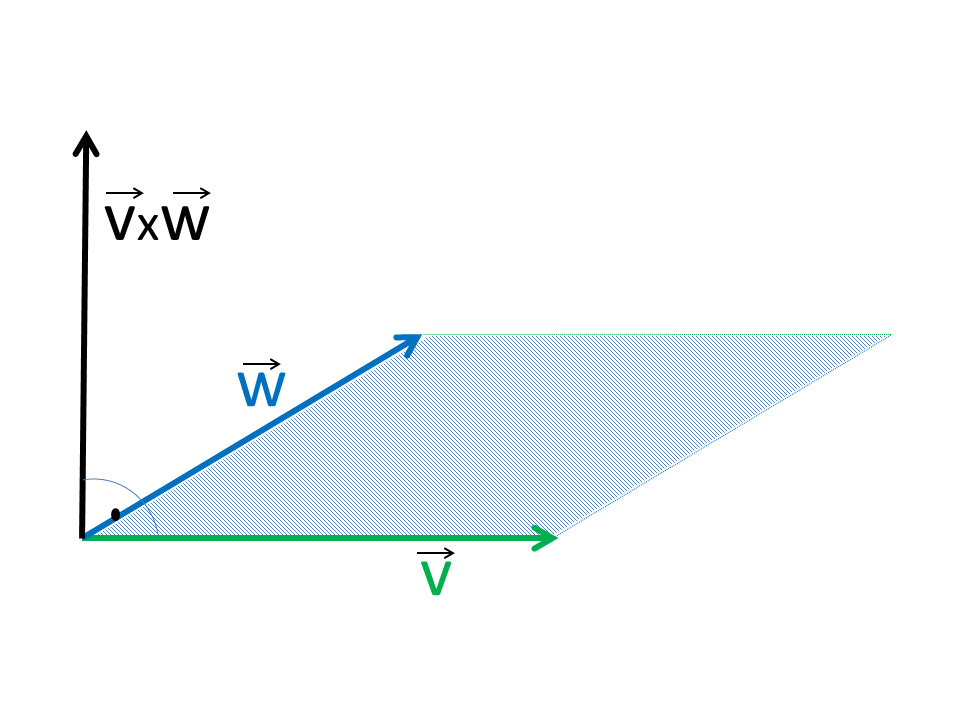
Das Vektorprodukt liefert als Ergebnis einen Vektor der senkrecht auf der durch die beiden Vektoren aufgespannten Fläche steht und dessen Länge dem Flächeninhalt des aufgespannten Parallelogramms entspricht. Das Vektorprodukt läßt sich auch geometrisch ausdrücken. Dabei ist φ der von den Vektoren eingeschlossene Winkel und n der Vektor senkrecht zur Fläche.
Das Vektorprodukt ist im dreidimensionalen euklidischen Vektorraum folgendermaßen definiert.
Das Vektorprodukt ist anti-Kommutativ
Multiplikation eines Vektors mit einer Matrix
Das Produkt einer Matrix mit einem Vektor ist eine lineare Abbildung. Erklärt ist die Multiplikation wenn die Anzahl der Spalten der Matrix gleich der Anzahl der Elemente des Vektors ist. Das Ergebnis ist ein Vektor dessen Anzahl der Komponenten der Anzahl der Zeilen der Matrix entspricht. D.h. das z.B. eine Matrix mit 2 Zeilen einen Vektor immer auf einen Vektor mit zwei Komponenten abbildet.
Mehrfachprodukte
Mehrfachprodukte von Vektoren sind im Allgemeinen nicht Assoziativ. D.h. im Allgemeinen gilt, dass die Reihenfolge in der die Produkte ausgeführt werden relevant ist.
Allgemein ist:
und
Für das doppelte Vektorprodukt gilt der Entwicklungssatz:
Das Spatprodukt ist gleich dem Volumen des durch die drei Vektoren aufgespannten Parallelepipeds. Das Spatprodukt ist positiv, wenn die drei Vektoren ein Rechtssystem bilden.
Lagrangesche Identität:
Geometrische Anwendungen
Gleichung der Geraden durch die zwei Punkte P0 und P1 gegeben durch die Vektoren r0 und r1:
Abstand der Punkte P0 and P1:
Weitere Seiten zum Thema
Hier einige weitere Seiten:
Index Matrizenrechnung Determinantenrechnung Vektoraddition grafisch Vektorsubtraktion grafisch Matrix-Vektorprodukt grafisch Skalarprodukt grafisch