Elementare Funktionen

Eigenschaften

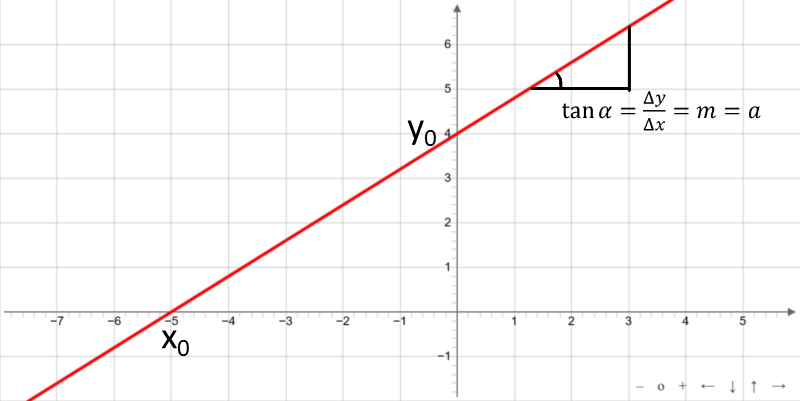
Lineare Funktionen sind ganze rationale Funktionen. Sie wachsen monoton für a > 0 und fallen monoton für a < 0. Bilder der linearen Funktionen sind Geraden.

Die lineare Funktion schneidet die x-Achse bei x₀

$f\left(x_0\right)=0$

$a·x_0+b=0$

$x_0=-\frac{b}{a}$

Die lineare Funktion schneidet die y-Achse bei y₀

$f\left(0\right)=y_0=b$

Die Steigung m der linearen Funktion ist gegeben durch den Parameter a.

$m=\tan \alpha =\frac{\Delta y}{\Delta x}=\frac{f\left(x\mathrm{+}\Delta x\right)\mathrm{-}f\left(x\right)}{\Delta x}=a$

a =

b =

Eigenschaften

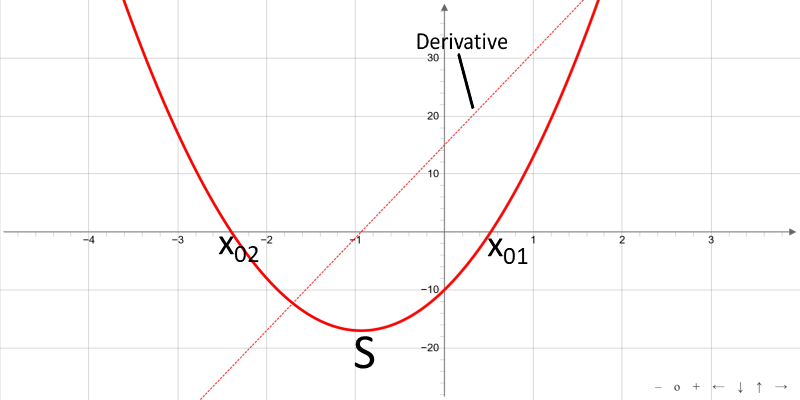
Quadratische Funktionen sind ganze rationale Funktionen zweiten Grades. Das Bild einer quadratischen Funktion ist eine Parabel, die nach oben bzw. nach unten geöffnet ist. Für a > 0 ist die Parabel nach oben geöffnet, für a < 0 nach unten.

Nullstellen

$x_{01,02}=-\frac{p}{2}\pm \sqrt{{\left(\frac{p}{2}\right)}^2-\mathrm{q}}$

mit

$p=\frac{b}{a}\text{und}q=\frac{c}{a}$

Scheitelpunt S

$S=\left(x_s{y}_s\right)=\left(-\frac{b}{2a}c-\frac{c^2}{4a}\right)$

Ableitung f′

$f\prime \left(x\right)=2ax+b$

Produktdarstellung

$f\left(x\right)=(x-x_{01})(x-x_{02})$

a =

b =

c =

Eigenschaften

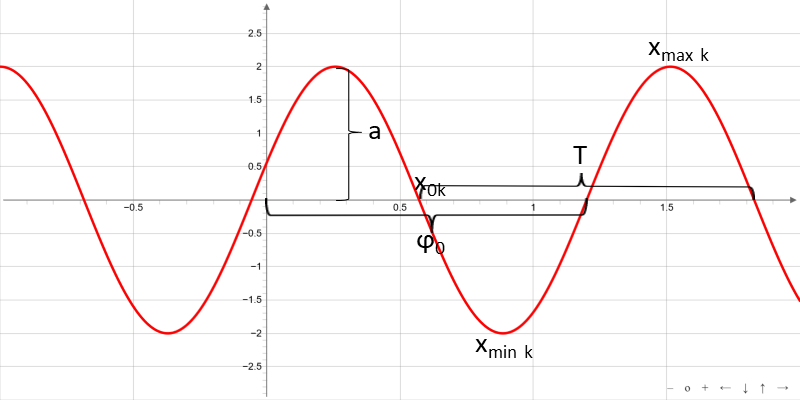
Für a = b = 1 und c = 0 liegt die gewöhnliche Sinusfunktion f(x) = sin(x) vor. Sie ist eine periodische Funktion mit der Periode 2 π und dem Wertebereich -1 ≤ f(x) ≤ 1.

Die allgemeine Sinusfunktion geht durch eine affine Transformation aus der gewöhnlichen Sinusfunktion hervor. Streckung mit dem Faktor a in Richtung der y-Achse, Streckung mit dem Faktor 1/b in Richtung der x-Achse und anschließende Parallelverschiebung in Richtung der x-Achse um -c/b.

Häufig werden die Parameter der allgemeinen Sinusfunktion folgendermaßen benannt:

$f\left(x\right)=A\sin (\omega x+{\phi }_0)$

dabei bezeichnet A die Amplitude, ω die Kreisfrequenz und φ₀ die Anfangsphase.

Viele Vorgänge in Natur und Technik, die den Charakter von Schwingungen tragen, lassen sich durch die allgemeine Sinusfunktion beschreiben.

Ist die Variable der allgemeinen Sinusfunktion die Zeit t dann spricht man von einer harmonischen Schwingung:

$f\left(t\right)=A\sin (\omega t+{\phi }_0)$

mit der Phasenverschiebung φ₀, der Amplitude A, der Schwingungsdauer T = 2 π / ω und der Frequenz f = 1 / T .

a =

b =

c =

Eigenschaften

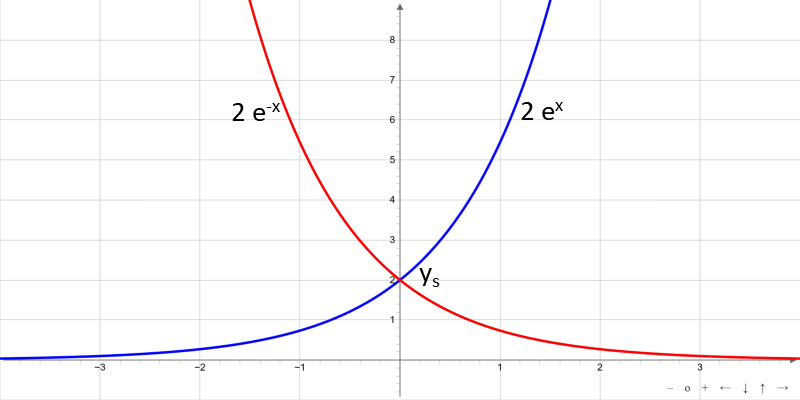
Die Exponentialfunktion ist für alle reellen Zahlen definiert. Die Funktion hat keine Nullstelle und keine Extrema. Die Funktionswerte sind stets positiv und die Funktion ist für b > 0 monoton steigend und für b < 0 monoton fallend. Die natürliche Exponentialfunktion e^x liegt vor für b = 1.

Für die Exponentialfunktion gilt das Additionstheorem:

$f(x_1+x_2)=f\left(x_1\right)+f\left(x_2\right)$

Die Inverse der Exponentialfunktion f(x) = a^x ist der Logarithmus:

$f^{-1}\left(x\right)={\log }_a\left(x\right)$

Im Spezialfall f(x) = e^x ist die Inverse der Logaritmus naturalis:

$f^{-1}\left(x\right)={\log }_e\left(x\right)=\ln \left(x\right)$

Anwendungen

Beschreibung des organischen Wachstums: mit g₀ Anfangsgröße und c der Wachstumskonstanten

$g\left(t\right)=g_0{e}^{ct}$

Exponential growth differential equation

Beschreibung eines Zerfallsprozesses: mit m₀ Anfangsgröße und λ der Zerfallskonstanten

$m\left(t\right)=m_0{e}^{-\lambda t}$

Gedämpfte Schwingung: mit der Dämfungskonstanten R

$f\left(t\right)=e^{-Rt}\sin (\omega t+{\phi }_0)$

b =

c =

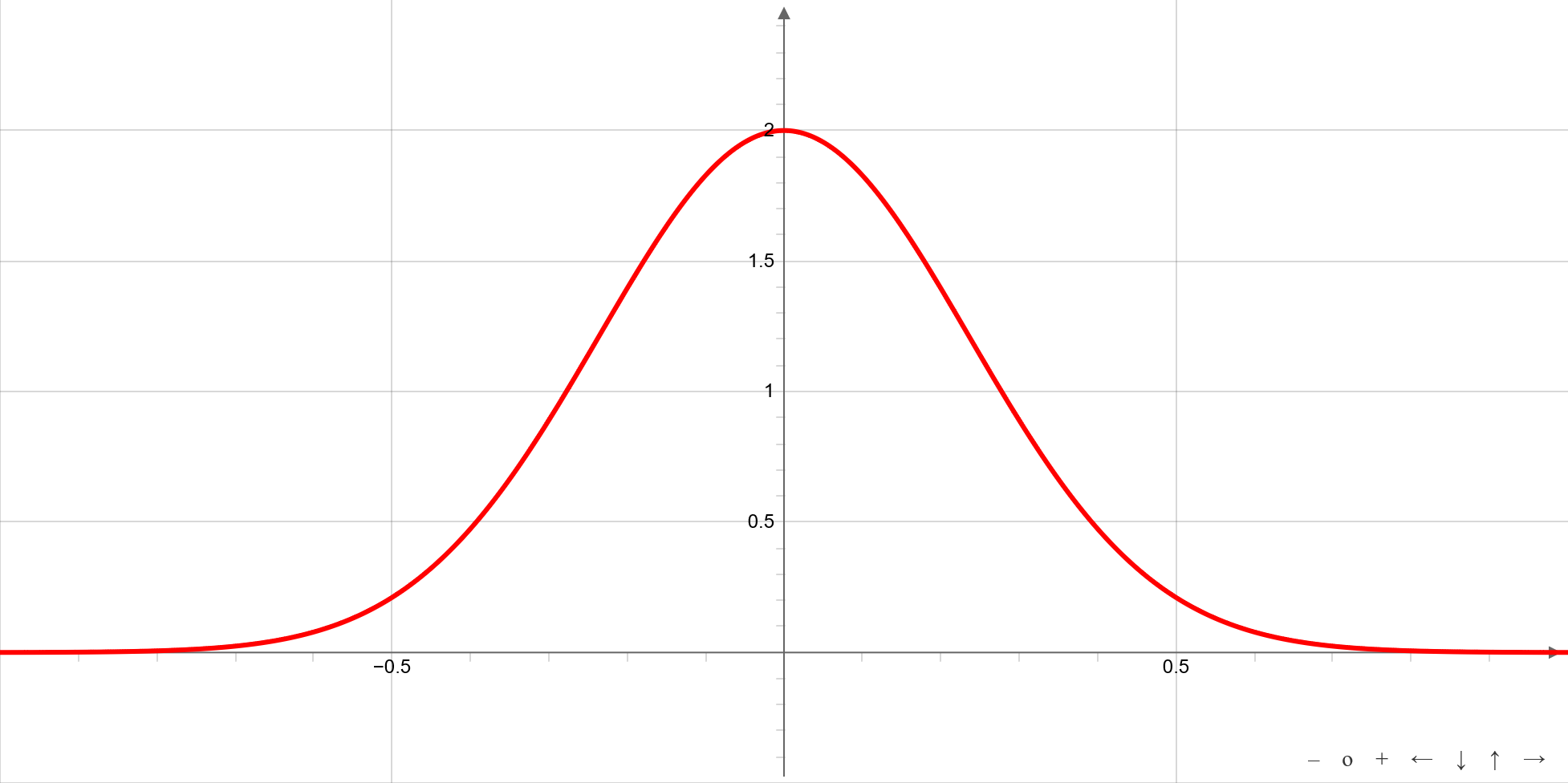
Eigenschaften

Die Funktion ist für jeden reellen Wert x definiert und nimmt ihr Maximum bei x = 0 mit y = b an. Das Bild der Funktion ist symmetrisch zur y-Achse.

Ableitung:

$f\prime \left(x\right)=-2a^{2}bx{e}^{-{\left(ax\right)}^2}$

Wendepunkte:

$x_{\mathrm{w1}}=\frac{1}{a\sqrt{2}};y_{\mathrm{w1}}=\frac{b}{\sqrt{e}}$

$x_{\mathrm{w2}}=-\frac{1}{a\sqrt{2}};y_{\mathrm{w2}}=\frac{b}{\sqrt{e}}$

Steigung der Wendetangenten:

${f\prime }_{\mathrm{w1}}=ab\cdot \sqrt{\frac{2}{e}}$

${f\prime }_{\mathrm{w2}}=-ab\cdot \sqrt{\frac{2}{e}}$

Spezialfall

Für

$b=\frac{1}{\sqrt{2\mathrm{\pi }}};a=\frac{1}{\sqrt{2}}$

liegt die Gaußsche Glockenkurve vor. Sie beschreibt die Wahrscheinlichkeitsdichte der Normalverteilung.

a =

b =

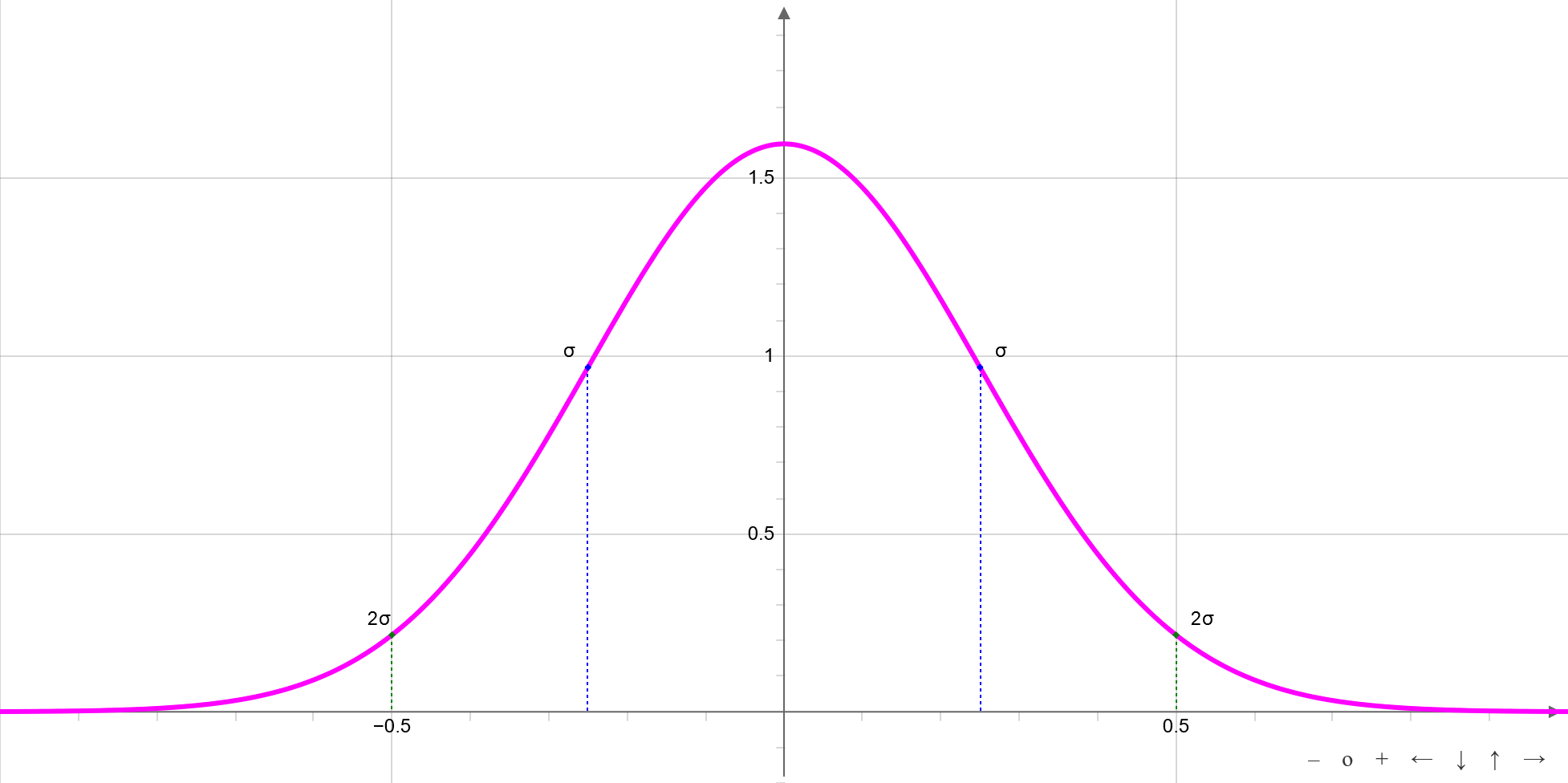
Eigenschaften

Das Bild der Gaußverteilung ist eine Glockenkurve mit dem Maximum und dem Symetriezentrum bei a. Der Parameter σ definiert den Abstand der Wendepunkte vom Symetriezentrum. Ist σ klein, dann ist die Glockenkurve schmal und spitz. Für große σ wird die Funktion flach und breit.

a =

σ =