Plot komplexer Funktionen mit der Farbkreismethode

Einstellungen für das Plotten

Farbton (hue)

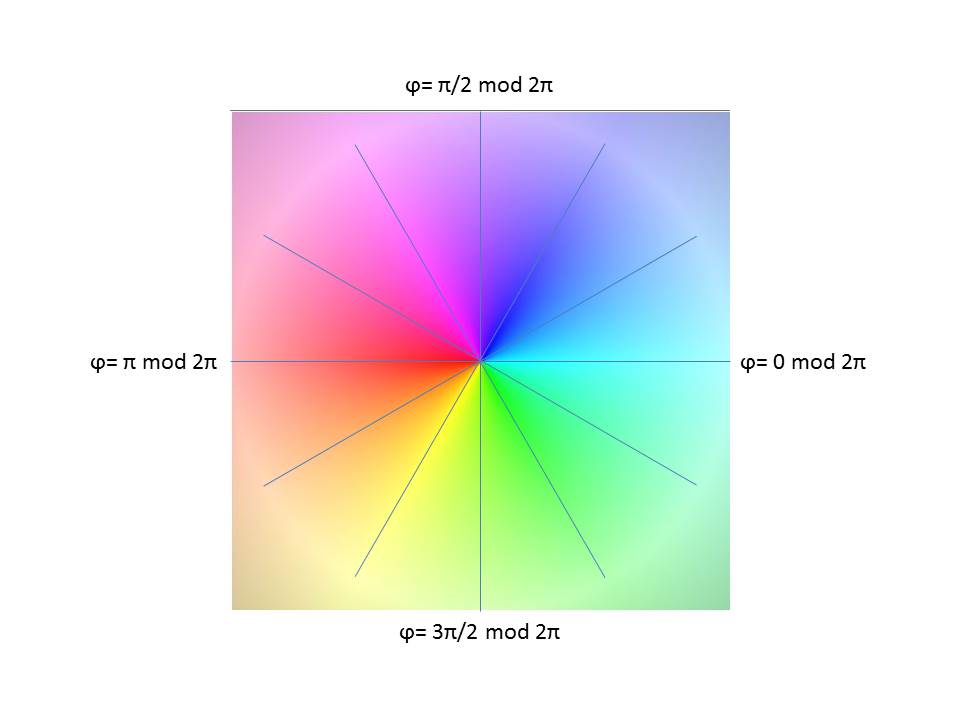
Der Farbton wird entsprechend des Winkels ausgewählt.

Helligkeit (lightness)

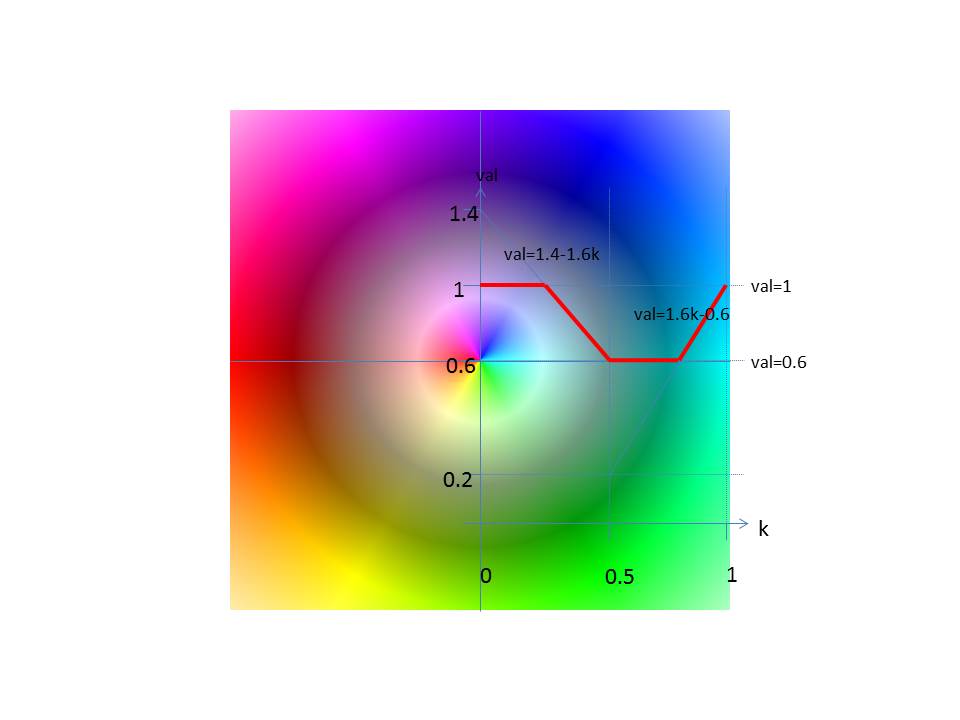
Die Helligkeit wird gemäß folgendem Diagramm bestimmt.

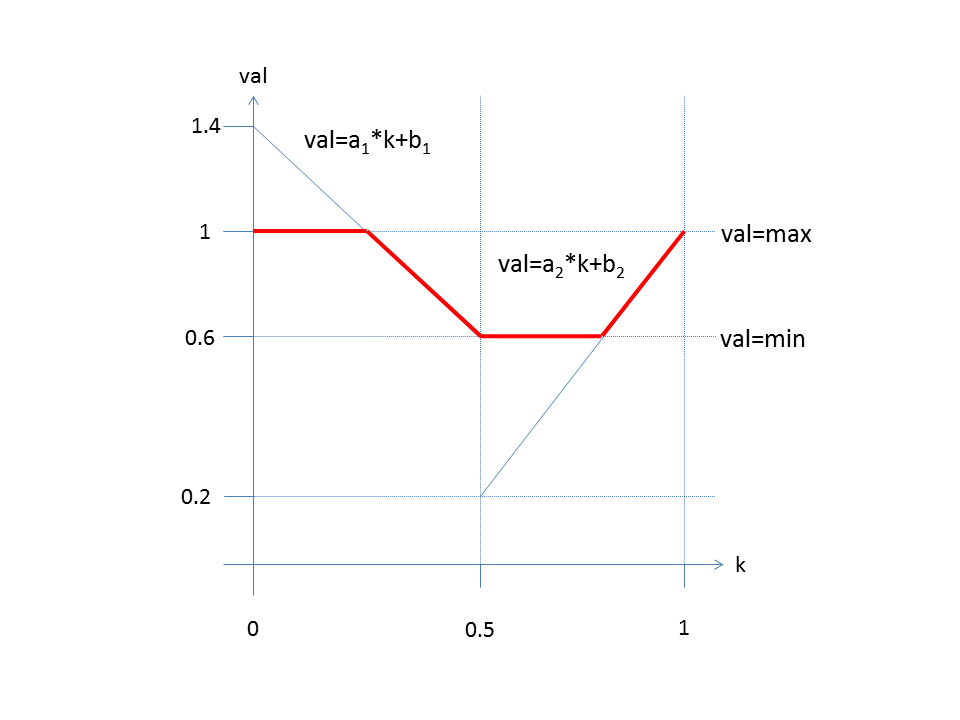
Im Intervall [0,0.5) gilt val = a₁ * k + b₁

Im Intervall [0.5,1) gilt val = a₂ * k + b₂

Es ist: min ≤ val ≤ max

Sättigung (saturation)

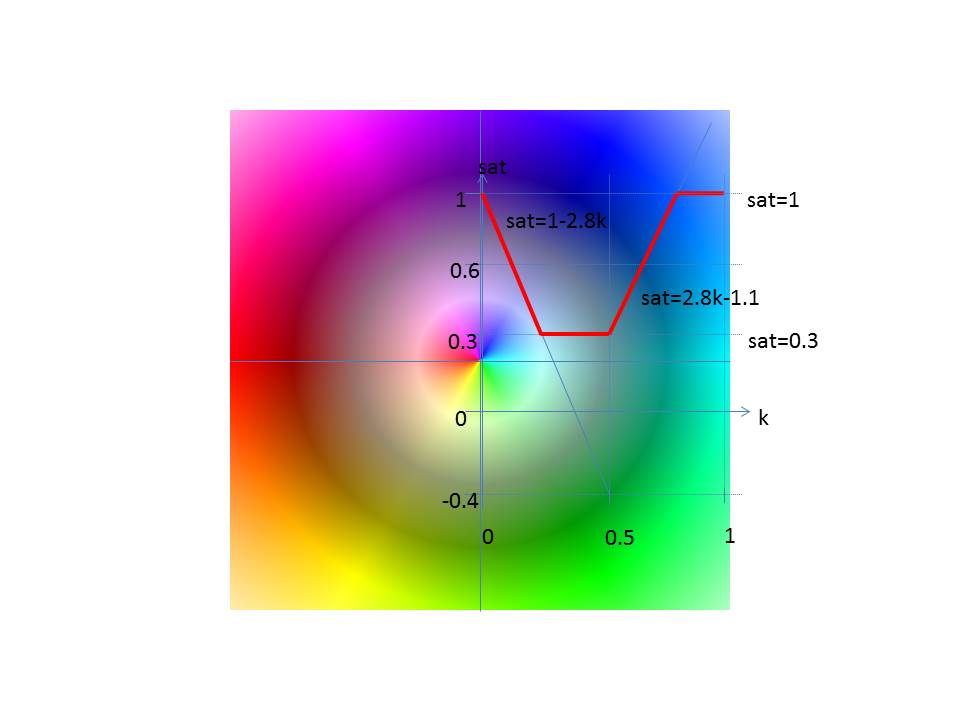
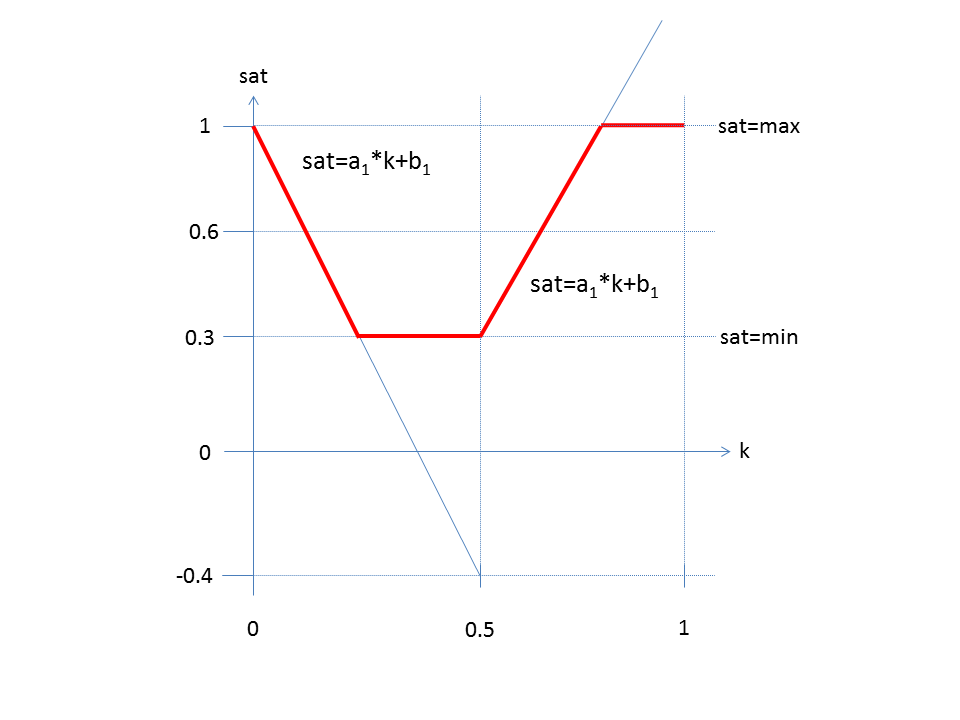
Die Sättigung wird gemäß folgendem Diagramm bestimmt.

Im Intervall [0,0.5) gilt sat = a₁ * k + b₁

Im Intervall [0.5,1) gilt sat = a₂ * k + b₂

Es ist: min ≤ sat ≤ max

Auswahl eines Farbschemas

Höhe und Breite der Grafik:

Einstellung der Sättigungsgradienten:

Einstellung der Helligkeitsgradienten:

Darstellung komplexer Funktionen

Lineare komplexe Funktion

$f (z) = z = x + i y$

$mit z \in C$

Realteil von f(z):

$Re (f (z)) = x$

Imaginärteil von f(z):

$Im (f (z)) = y$

Betrag von f(z):

$| f (z) | = \sqrt{x^{2} + y^{2}}$

Argument φ von f(z):

$φ (f (z)) = atan \frac{x}{y}$

Quadratische komplexe Funktion

$f (z) = z^{2}$

$mit z \in C$

Realteil von f(z):

$Re (f (z)) = x^{2} - y^{2}$

Imaginärteil von f(z):

$Im (f (z)) = 2 x y$

Betrag von f(z):

$| f (z) | = x^{2} + y^{2}$

Argument φ von f(z):

$φ (f (z)) = atan \frac{2 x y}{x^{2} - y^{2}}$

Gebrochen rationale komplexe Funktion

$f (z) = \frac{1}{z - a}$

$mit z \in C und a = α + i β$

Realteil von f(z):

$Re (f (z))$ $= \frac{x - α}{{(x - α)}^{2} - {(y - β)}^{2}}$

Imaginärteil von f(z):

$Im (f (z))$ $= \frac{- (y - β)}{{(x - α)}^{2} - {(y - β)}^{2}}$

Betrag von f(z):

$| f (z) |$ $= \frac{1}{\sqrt{{(x - α)}^{2} - {(y - β)}^{2}}}$

Argument φ von f(z):

$φ (f (z)) = atan \frac{y - β}{α - x}$

Gebrochen lineare Funktion

$f (z) = \frac{z + a}{z + b}$

$mit z \in C und a = α + i β; b = γ + i δ$

Realteil von f(z):

$Re (f (z))$ $= \frac{(x + α) (x + γ) + (y + β) (y + δ)}{{(x + γ)}^{2} + {(y + δ)}^{2}}$

Imaginärteil von f(z):

$Im (f (z))$ $= \frac{(y + β) (x + γ) - (y + δ) (x + α)}{{(x + γ)}^{2} + {(y + δ)}^{2}}$

$f (z) = \frac{1}{z - a} + \frac{1}{z - b}$

$mit z \in C und a = α + i β; b = γ + i δ$

Die Funktion f ist eine Zusammensetzung der vorherigen f=f₁+f₂ und so ergeben sich Real- und Imaginärteil aus der Addition der einzelnen Funktionen f₁ und f₂.

Realteil von f(z):

$Re (f_{1} + f_{2}) = Re (f_{1}) + Re (f_{2})$

Imaginärteil von f(z):

$Im (f_{1} + f_{2}) = Im (f_{1}) + Im (f_{2})$

Komplexe e-Funktion

$f (z) = e^{z}$

$mit z \in C$

Realteil von f(z):

$Re (f (z)) = e^{x} \cos y$

Imaginärteil von f(z):

$Im (f (z)) = e^{x} \sin y$

Betrag von f(z):

$| f (z) | = e^{x}$

Argument φ von f(z):

$φ (f (z)) = y + 2 n π$

exp(z) / (z-a)

$f (z) = \frac{e^{z}}{z - a}$

$mit z \in C und a = α + i β$

Die Funktion f ist ein Produkt zweier Funktionen f=f₁ * f₂ und so ergeben sich Real- und Imaginärteil folgendermaßen:

Realteil von f(z):

$Re (f_{1} * f_{2}) = Re (f_{1}) Re (f_{2}) - Im (f_{1}) Im (f_{2})$

Imaginärteil von f(z):

$Im (f_{1} * f_{2}) = Re (f_{1}) Im (f_{2}) + Re (f_{2}) Im (f_{1})$

exp(z)/(z-a) + (z+b)/(z+c)

$f (z) = \frac{e^{z}}{z - a} + \frac{z + b}{z + c}$

$mit z \in C und a = α + i β; b = γ + i δ; c = ε + i ζ$

Die Funktion f ist ein Produkt zweier Funktionen f=f₁ * f₂ und so ergeben sich Real- und Imaginärteil folgendermaßen:

Realteil von f(z):

$Re (f_{1} * f_{2}) = Re (f_{1}) Re (f_{2}) - Im (f_{1}) Im (f_{2})$

Imaginärteil von f(z):

$Im (f_{1} * f_{2}) = Re (f_{1}) Im (f_{2}) + Re (f_{2}) Im (f_{1})$

Die Funktion f ist außerdem die Summe zweier Funktionen f=f₁+f₂ und so ergeben sich Real- und Imaginärteil aus der Addition der einzelnen Summunden f₁ und f₂.

Realteil von f(z):

$Re (f_{1} + f_{2}) = Re (f_{1}) + Re (f_{2})$

Imaginärteil von f(z):

$Im (f_{1} + f_{2}) = Im (f_{1}) + Im (f_{2})$

Komplexe Sinusfunktion

$f (z) = \sin z$

$mit z \in C$

Realteil von f(z):

$Re (f (z)) = \sin x \cosh y$

Imaginärteil von f(z):

$Im (f (z)) = \cos x \sinh y$

Betrag von f(z):

$| f (z) | = \sqrt{\sin^{2} x + \sinh^{2} y}$

Argument φ von f(z):

$φ (f (z)) = atan (\cot x \tanh y)$

x² + i y²

$f (z) = x^{2} + i y^{2}$

Realteil von f(z):

$Re (f (z)) = x^{2}$

Imaginärteil von f(z):

$Im (f (z)) = y^{2}$

Betrag von f(z):

$| f (z) | = \sqrt{x^{2} + y^{2}}$

Argument φ von f(z):

$φ (f (z)) = atan \frac{y^{2}}{x^{2}}$

Allgemein

Die Funktionentheorie untersucht Funktionen einer komplexen Veränderlichen also Funktionen komplexer Zahlen, deren Wertebereich ebenfalls komplexe Zahlen sind. Die komplexen Zahlen sind eine Erweiterung der reellen Zahlen in den zweidimensionalen Raum. Viele Rechenregeln der reellen Zahlen lassen sich auf komplexe Zahlen übertragen. Begründet wurde die Theorie der komplexen Funktionen im Wesentlichen durch Augustin-Louis Cauchy, Bernhard Riemann und Karl Weierstraß.

Farbkreismethode

Die Farbkreismethode (complex color wheel method oder domain coloring) ist ein Verfahren um komplexe Funktionen grafisch darzustellen. Komplexe Funktionen bilden die komplexe Ebene in wiederum zweidimensionale Werte mit Real- und Imaginärteil ab. Die Farbkreismethode verwendet Betrag r=|f(z)| und Winkel φ des komplexen Funktionswertes f(z) um die Darstellungsfarbe des Funktionswertes festzulegen. Gemäß r und φ des Funktionswertes wird die Farbe aus dem Farbkreis ausgewählt. Der Betrag definiert die Sättigung und wird Modulo auf Intervalle abgebildet. Das erste Interval ist 0...1 dann folgen die Intervalle (1...e], (e...e²], (e²...e³] usw. Der Farbton ist durch den Winkel definiert und in 6 Farbzonen aufgeteilt beginnend mit blau von 0° bis 60° und endend mit grün von 300° bis 360°. Die Methode ist so angelegt, dass Funktionswerte die nah beieinander liegen auch farblich ähnlich dargestellt werden. Die Abbildung der Beträge auf Intervalle der Potenz von e entspricht einer logarithmischen Darstellung.

Farbkreis

Die Zusammenstellung eines Farbkreises kann unter verschiedenen Gesichtspunkten zusammengestellt werden je nachdem welcher Sachverhalt visualisiert werden soll. Grundlage für den Farbkreis ist die Wahrnehmung ähnlicher Farben. Lässt man normalsichtige Versuchspersonen Farbmuster nach der Empfindung auf Ähnlichkeit sortieren, werden die Farbtöne in der Regel in dieselbe Reihenfolge gebracht. Anfang und Ende der Reihe sind sich dabei so ähnlich, dass die Reihe zu einem Kreis geschlossen werden kann.

Gauss Plane

The complex numbers are two-dimensional und can be used as vectors in the Gaussian plane of numbers represent. On the horizontal axis (Re) of the real part und on the vertical axis is applied (Im) of the imaginary part of the complex number. Vectors may also be similar to either the complex number in Cartesian coordinates (x, y) or polar coordinates (r, φ) can be expressed. In the color circle method polar coordinates are used und the color wheel is placed on the manner interval Gaussian-number plane.

Weitere Seiten zum Thema

Hier ist eine Liste weiterer nützlicher Seiten:

Index Elementare Funktionen Funktionen Plotter Parabel Plotter Kubische Funktion Plotter Gaußverteilung Plotter Sinus Plotter Kosinus Plotter Tangens Plotter Schwebungen Plotter Komplexe Funktionen Regression Mittelwertrechner

Plot komplexer Funktionen mit der Farbkreismethode

Einstellungen für das Plotten

Farbton (hue)

Helligkeit (lightness)

Sättigung (saturation)

Darstellung komplexer Funktionen

Allgemein

Farbkreismethode

Farbkreis

Gauss Plane

Links

Weitere Seiten zum Thema