Komplexe Zahlen

Definitionen und Schreibweisen für komplexe Zahlen

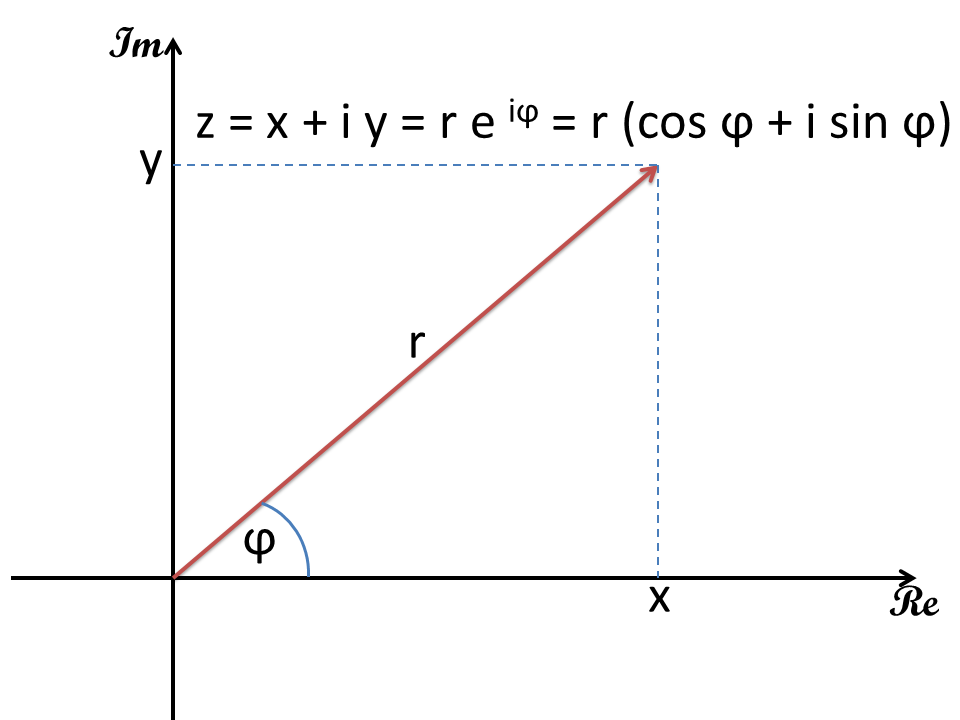
Die komplexen Zahlen sind eine Erweiterung der reellen Zahlen. Viele Rechenregeln der reellen Zahlen lassen sich auf komplexe Zahlen übertragen.

Die Theorie der analytischen Funktionen behandelt Funktionen mit einer komplexen Veränderlichen.

Die Enstehung der komplexen Zahlen geht auf das Lösen algebraischer Gleichungen zurück. Der Ursprung der Theorie der imaginären Zahlen, das heißt aller Zahlen, deren Quadrat eine negative reelle Zahl ist, geht auf die italienischen Mathematiker Gerolamo Cardano und Rafael Bombelli bis ins 16. Jahrhundert zurück. Die Einführung der imaginären Einheit i als neue Zahl wird Leonhard Euler zugeschrieben.

Die komplexen Zahlen sind zweidimensional und lassen sich als Vektoren in der gaußschen Zahlenebene darstellen. Auf der horizontalen Achse (Re) wird der Realteil und auf der senkrechten Achse (Im) der Imaginärteil der komplexen Zahl aufgetragen. Analog zu Vektoren kann auch die komplexe Zahl entweder in kartesischen Koordinaten (x, y) oder in Polarkoordinaten (r, φ) ausgedrückt werden.

Eine komplexe Zahl z besteht aus einem Realteil x und einem Imaginärteil y. Der Imaginärteil wird durch die imaginäre Einheit i gekennzeichnet.

$z = x + i y$

$mit x, y \in R and i = \sqrt{-1}$

Die zu z konjugiert komplexe Zahl besteht aus einem Realteil x und dem negativen Imaginärteil y. Das entspricht einer Spiegelung an der reellen Achse in der Gaußschen Zahlenebene.

$\overline{z} = x - i y$

Dem Betrag einer komplexe Zahl entspricht in der Gaußschen Zahlenebene die Länge des Vektors z.

$| z | = \sqrt{x^{2} + y^{2}}$

Die komplexe Zahl in Polarkoordinaten:

$z = r (\cos φ + i \sin φ) = r e^{i φ}$

mit

$r = | z | = \sqrt{x^{2} + y^{2}}$

und

$φ = atan \frac{y}{x}$

und der Eulerschen Formel

$\cos φ + i \sin φ = e^{i φ}$

Grafische Darstellung der komplexen Zahl

Beziehungen konjugiert komplexer Zahlen

Für konjugiert komplexe Zahlen gelten die folgenden Beziehungen.

$\overline{z} = z wenn z reell ist;$

$\overline{z_{1} + z_{2}} = \overline{z_{1}} + \overline{z_{2}}$

$\overline{z_{1} \cdot z_{2}} = \overline{z_{1}} \cdot \overline{z_{2}}$

$\overline{(\frac{z_{1}}{z_{2}})} = \frac{\overline{z_{1}}}{z_{2}}$

$z \cdot \overline{z} = x^{2} + y^{2}$

Rechenregeln für komplexe Zahlen

Addition und Subtraktion komplexer Zahlen

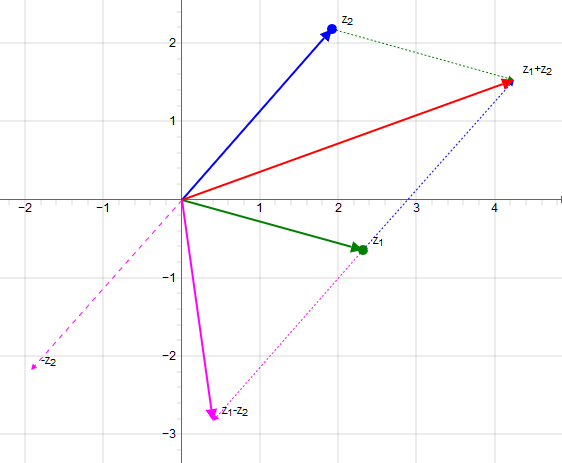
Die Addition und Subtraktion komplexer Zahlen entspricht der Addition und Subtraktion der Ortsvektoren. D.h. die real- und imaginär Komponenten werden addiert bzw. subtrahiert.

$Mit z_{1} = x_{1} + i y_{1} and z_{2} = x_{2} + i y_{2} ist$

$z_{1} + z_{2} = x_{1} + x_{2} + i (y_{1} + y_{2})$

$z_{1} - z_{2} = x_{1} - x_{2} + i (y_{1} - y_{2})$

Grafische Addition komplexer Zahlen

Multiplikation komplexer Zahlen

Die Multiplikation erfolgt, indem die Klammern unter Berücksichtigung der Beziehung i²= -1 ausmultipliziert werden.

$Mit z_{1} = x_{1} + i y_{1} und z_{2} = x_{2} + i y_{2} ist$

$z_{1} \cdot z_{2} = (x_{1} + i y_{1}) \cdot (x_{2} + i y_{2})$ $= x_{1} \cdot x_{2} - y_{1} \cdot y_{2} + i (x_{1} \cdot y_{2} + y_{1} \cdot x_{2})$

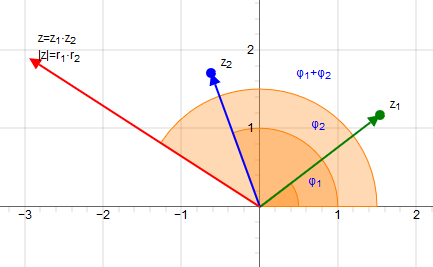
Die Multiplikation komplexer Zahlen kann auch in trigonometrischer bzw. exponentieller Form erfolgen.

$Mit z_{1} = r_{1} (\cos φ + i \sin φ) = r_{1} e^{i φ}$

$und z_{2} = r_{2} (\cos ψ + i \sin ψ) = r_{2} e^{i ψ} ist$

$z_{1} \cdot z_{2}$ $= r_{1} r_{2} (\cos (φ + ψ) + i \sin (φ + ψ))$ $= r_{1} r_{2} e^{i (φ + ψ)}$

Grafische Multiplikation komplexer Zahlen

Rechner: Multiplikation komplexer Zahlen

Division komplexer Zahlen

Die Division erfolgt, indem der Bruch mit dem konjugiert komplexen des Nenners erweitert wird.

$Mit z_{1} = x_{1} + i y_{1} und z_{2} = x_{2} + i y_{2} ist$

$\frac{z_{1}}{z_{2}} = \frac{x_{1} + i y_{1}}{x_{2} + i y_{2}}$ $= \frac{x_{1} + i y_{1}}{x_{2} + i y_{2}} \frac{x_{2} - i y_{2}}{x_{2} - i y_{2}}$ $= \frac{x_{1} x_{2} + y_{1} y_{2}}{x_{2}^{2} + y_{2}^{2}} + i \frac{x_{2} y_{1} - x_{1} y_{2}}{x_{2}^{2} + y_{2}^{2}}$

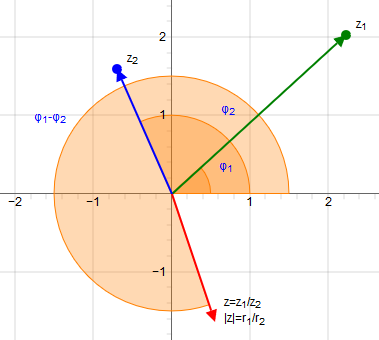
Die Division komplexer Zahlen kann auch in trigonometrischer bzw. exponentieller Form erfolgen.

$Mit z_{1} = r_{1} (\cos φ + i \sin φ) = r_{1} e^{i φ}$

$and z_{2} = r_{2} (\cos ψ + i \sin ψ) = r_{2} e^{i ψ} ist$

$\frac{z_{1}}{z_{2}}$ $= \frac{r_{1}}{r_{2}} (\cos (φ - ψ) + i \sin (φ - ψ))$ $= \frac{r_{1}}{r_{2}} e^{i (φ - ψ)}$

Grafische Division komplexer Zahlen

Rechner: Division komplexer Zahlen

Elementare Funktionen f(z)

Komplexe Zahl kartesisch

$z = x + i y$

Realteil

$Re(z) = x$

Imaginärteil

$Im(z) = y$

Konjugiert komplexe Zahl

$\overline{z} = x - i y$

Betrag

$| z | = \sqrt{x^{2} + y^{2}}$

Argument

$arg(z) = φ = atan \frac{y}{x}$

Polar

$z = | z | (\cos φ + i \sin φ)$

Quadrat

$z^{2} = x^{2} - y^{2} + i x y$

Kehrwert

$\frac{1}{z} = \frac{x}{x^{2} + y^{2}} + i \frac{-y}{x^{2} + y^{2}}$

Quadratischer Kehrwert

$\frac{1}{z^{2}} = \frac{x^{2} - y^{2}}{{(x^{2} + y^{2})}^{2}} + i \frac{- 2 x y}{{(x^{2} + y^{2})}^{2}}$

Wurzel

$\sqrt{z} = \pm \sqrt{\frac{x + \sqrt{x^{2} + y^{2}}}{2}} \pm i \sqrt{\frac{- x + \sqrt{x^{2} + y^{2}}}{2}}$

Exponentialfunktion

$e^{z} = e^{x} \cos y + i e^{x} \sin y$

Logarithmus

$\ln z = \frac{1}{2} \ln (x^{2} + y^{2}) + i atan \frac{y}{x}$

Sinus

$\sin z = \sin x \cosh y + i \cos x \sinh y$

Cosinus

$\cos z = \cos x \cosh y - i \sin x \sinh y$

Sinus Hyperbolicus

$\sinh z = \sinh x \cos y + i \cosh x \sin y$

Cosinus Hyperbolicus

$\cosh z = \cosh x \cos y - i \sinh x \sin y$

Tangens

$\tan z = \frac{\sin 2 x}{\cos 2 x + \cosh 2 y} + i \frac{\sinh 2 y}{\cos 2 x + \cosh 2 y}$

Komplexe Zahlen Online Rechner

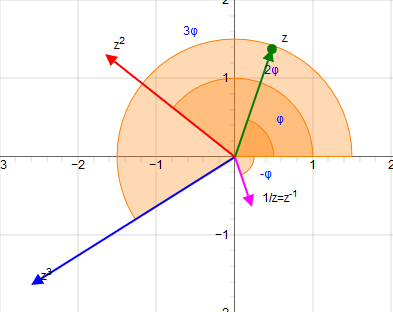
Potenzen komplexer Zahlen

Das Erheben einer komplexen Zahl in die n-te natürliche Potenz erfolgt nach der Formel von Moivre.

$z^{n}$ $= r^{n} (\cos n φ + i \sin n φ)$ $= r^{n} e^{i n φ}$

$mit r = | z | = \sqrt{x^{2} + y^{2}}$

$und φ = atan \frac{y}{x}$

$und i^{0} = 1, i^{1} = i, i^{2} = - 1, i^{3} = - i ...$

$und n \in N$

oder algebraisch nach dem Binomischen Lehrsatz

$z^{n} = {(x + i y)}^{n} = \sum_{k = 0, k gerade}^{n} (\begin{matrix} n \\ k \end{matrix}) {(- 1)}^{\frac{k}{2}} x^{n - k} y^{k} + i \sum_{k = 1, k ungerade}^{n} (\begin{matrix} n \\ k \end{matrix}) {(- 1)}^{\frac{k - 1}{2}} x^{n - k} y^{k}$

Rechner: Binomischer Satz für komplexe Zahlen

Der Rechner berechnet die Potenz der komplexen Zahl nach dem Binomischen Satz.

Für beliebige komplexe Exponenten gilt:

$z^{ω} = e^{ω \ln z}$

mit z^ω wobei z^ω als Hauptwert zu verstehen ist. Ist ω irrational so gibt es unendlich viele Lösungen.

Grafisch Potenzen komplexer Zahlen

Rechner kartesische Form in Polarform

Rechner zur Umrechnung einer komplexen Zahl von der kartesischen Darstellung in die Polarform. Der Winkel ist in Radiant.

Kartesisch

Konjugiert

Betrag

Winkel

Polar

Rechner Polarform in kartesische Form

Rechner zur Umrechnung einer komplexen Zahl von der Polarform in die kartesische Darstellung. Der Winkel ist in Radiant.

Polar

Kartesisch

Konjugiert

Betrag

Komplexe Zahlen

Definitionen und Schreibweisen für komplexe Zahlen

Beziehungen konjugiert komplexer Zahlen

Rechenregeln für komplexe Zahlen

Addition und Subtraktion komplexer Zahlen

Multiplikation komplexer Zahlen

Rechner: Multiplikation komplexer Zahlen

Division komplexer Zahlen

Rechner: Division komplexer Zahlen

Elementare Funktionen f(z)

Potenzen komplexer Zahlen

Rechner: Binomischer Satz für komplexe Zahlen

Rechner kartesische Form in Polarform

Rechner Polarform in kartesische Form

Weitere Seiten zum Thema