Online Rechner Fourierreihe
Rechner zur Fourierreihenentwicklung an beliebige Messwerte oder Funktionen
Als Fourierreihe, nach Joseph Fourier (1768–1830), bezeichnet man die Reihenentwicklung einer periodischen, abschnittsweise stetigen Funktion in eine Funktionenreihe aus Sinus- und Kosinusfunktionen.
Mit dem Rechner kann eine Fourierreihenentwicklung an beliebige Messwerte erfolgen oder alternativ an eine Funktion.
Intervall
f(x)=
Bei der Fourierentwicklung einer Funktion kann der Intergrationsbereich angegeben werden (Intervall). Bei der Angabe von Punkten wird zwischen den Punkten linear interpoliert und der Integrationsbereich erstreckt sich vom ersten bis zum letzten angegebenen Punkt.
| Funktion | Beschreibung |
|---|---|
| sin(x) | Sinus |
| cos(x) | Cosinus |
| tan(x) | Tangens |
| asin(x) | Arcussinus |
| acos(x) | Arcuscosinus |
| atan(x) | Arcustangens |
| atan2(y, x) | Arcustangens von y/x |
| cosh(x) | Cosinus hyperbolicus |
| sinh(x) | Sinus hyperbolicus |
| pow(a, b) | Potenz ab |
| sqrt(x) | Quadratwurzel |
| exp(x) | e-Funktion |
| log(x), ln(x) | Natürlicher Logarithmus |
| log(x, b) | Logarithmus zur Basis b |
| log2(x), lb(x) | Logarithmus zur Basis 2 |
| log10(x), ld(x) | Logarithmus zur Basis 10 |
Eine alternative Eingabe ist über das Laden der Daten aus einer Datei möglich. Die Werte müssen durch Komma, Leerzeichen oder Semikolon getrennt sein und paarweise vorliegen x1, y1, x2, y2, ...
Parameter der Fourierreihe:
Fourierreihe
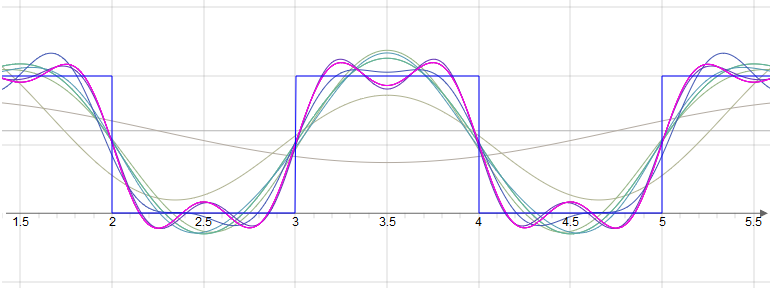
Messwerte können durch periodische Funktionen angenähert werden. Das Verfahren dazu ist die Entwicklung einer Fourierreihe. Die Elemente der Fourierreihe sind die Sinus- und Cosinusfunktionen. Die Entwicklung erfolgt nach aufsteigenden Frequenzen.
Die Fourierreihe lautet:
mit den Fourierkoeffizienten ak und bk und ω = 2π/T. Dabei ist Periode T = b - a mit dem Intervallanfang a und dem Intervallende b.
Die Fourierkoeffizienten ak und bk erfüllen die kleinste Quadrate Bedingung für die zugehörige Sinus- bzw. Cosinusfunktion. Die Koeffizienten berechnen sich wie folgt.
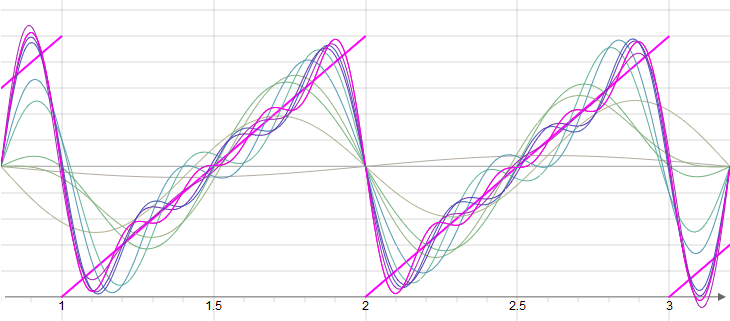
Beispiel: Sägezahnfunktion
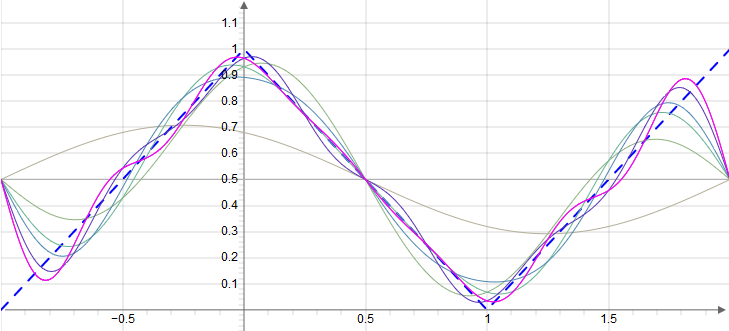
Beispiel: Dreiecksfunktion

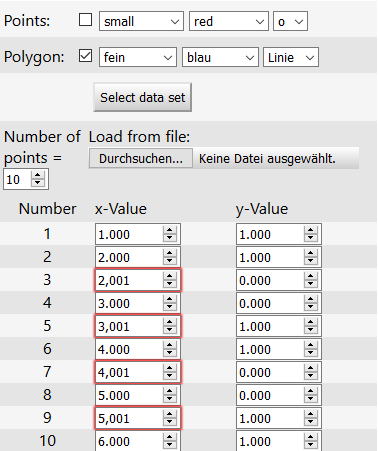
Beispiel: Rechteckfunktion
Druck und speicherbares Bild
Drucken oder Speichern der Abbildung mit Anwahl über die rechte Maustaste.
Weitere Seiten zum Thema
Hier ist eine Liste weiterer Seiten:
Index FFT Rechner Horner-Schema Lagrange Interpolation Ausgleichsgerade, Ausgleichspolynom, Fourierreihe, Potenzgesetz, Gaussfunktion. Mittelwertrechner Fitting Gaußverteilung Rechner Taylorreihe Lineare Dgl 1.Ordnung