Gleitende Durchschnitte SMA, WMA und EMA

Rechner zur Berechnung der gleitenden Durchschnitte SMA, WMA und EMA

Der gleitende Durchschnitt (auch gleitender Mittelwert) ist eine Methode zur Glättung von Zeit- bzw. Datenreihen. Die Glättung erfolgt durch das Entfernen höherer Frequenzanteile. Die Menge der gleitenden Durchschnitte wird iterativ („gleitend“) über einen Ausschnitt, das „Fenster“, eines gegebenen Signals berechnet. Das verwendete Fenster wird überlappend verschoben, d. h., wiederholt wird der letzte Wert aus dem betrachteten Ausschnitt gestrichen, der erste Wert nach dem Ausschnitt hinzugenommen und ein neuer Mittelwert berechnet.

Mit dem Rechner können die gleitenden Mittelwerte an beliebige Datenreihen berechnet werden. Die Datenreihe kann in eine Tabelle eingegeben werden oder aus einer Datei eingelesen werden. Die Periodenlänge kann beliebig gewählt und damit der Glättungsfaktor variiert werden. Unterschiedliche Glättungswerte können verglichen werden ebenso wie unterschiedliche Mittelwerte. Zu jedem Mittelwert kann die Standartabweichung (SD Standard Deviation) eingeblendet werden. Wahlweise können die Daten als Punkte oder Splinekurve dargestellt werden. Die berechneten Mittelwerte werden zusätzlich zur grafischen Darstellung in einer Tabelle numerisch aufgelistet. Die Ergebnisstabelle kann als csv-Datei exportiert werden.

⃢

Zoom-x

Zoom-y

Die Ergebnisstabelle wird mit dem Aufruf von 'Aktualisieren' neu berechnet.

Nr.

Data

SMA₁

SMA₂

WMA₁

WMA₂

EMA₁

EMA₂

EMA₃

Gleitender Durchschnitt GD (oder Simple Moving Average SMA)

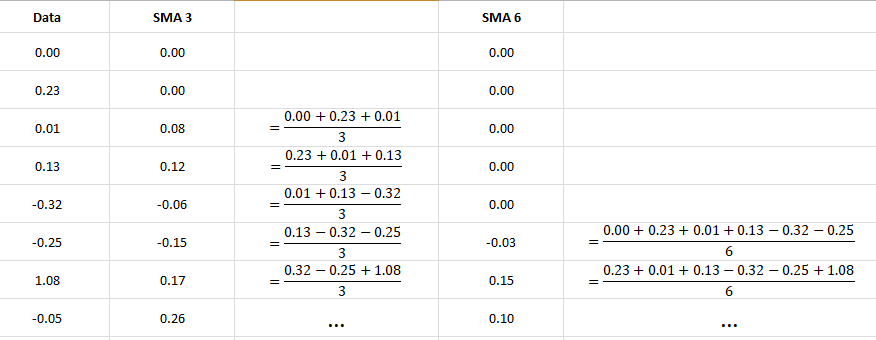
Berechnungsschema für den SMA mit den Periodenlängen 3 und 6

Berechnungsformel für den gleitenden Durchschnitt:

SMA_t= 1/n ⋅ ∑^t_i=t-n C_i

C_i: i-ter Wert der Datenreihe

n: Periodenlänge

Beim arithmetischen bzw. einfachen gleitende Durchschnitt (Simple Moving Average – SMA) werden einfach alle Datenpunkte eines betrachteten Zeitraums addiert und anschließend durch die Anzahl der Datenpunkte dividiert. Damit besitzt jeder einzelne Datenpunkt den gleichen Einfluss auf das Ergebnis. Durch die auf diese Weise berechnete Durchschnittslinie erfolgt eine Glättung des Kursverlaufs. Die Durchschnittslinie ist deswegen gleitend, weil mit jedem neu hinzukommenden Kurs in der Zeitreihe der älteste Kurs in der Berechnung wegfällt.

Linear gewichteter gleitender Durchschnitt (oder Linear Weighted Moving Average WMA)

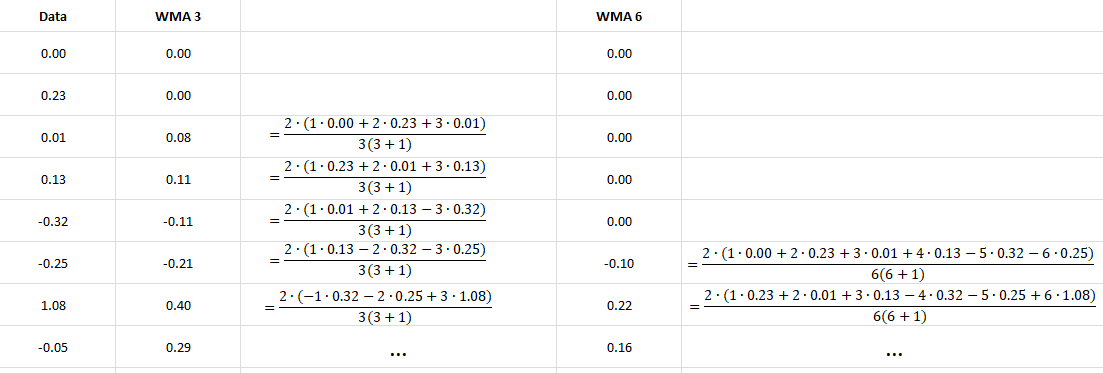
Berechnungsschema für den WMA mit den Periodenlängen 3 und 6

Berechnungsformel für den linear gewichteten gleitender Durchschnitt:

WMA_t= 2/(n(n+1)) ⋅ ∑ⁿ_i=1 i ⋅ C_t-n+i

C_i: i-ter Wert der Datenreihe

n: Periodenlänge

Beim linear gewichteten gleitenden Durchschnitt (Weighted Moving Average – WMA) werden die näheren Datenpunkte mit einem höheren Gewichtungsfaktor multipliziert als die ferneren Datenpunkte, wobei der Gewichtungsfaktor linear abnimmt bis zum ältesten Datenpunkt.

Exponentiell gleitender Durchschnitt (Exponential Moving Average EMA)

Berechnungsschema für den EMA mit den Periodenlängen 3 und 6 sowie dem Glättungsfaktor 0.6

Berechnungsformel für den exponentiell gleitenden Durchschnitt:

EMA_t= C_t * SF + (1 - SF) * EMA_t-1

mit

EMA_t: exponentiell gleitender Durchschnitt der betrachteten Periode

EMA_t-1: exponentiell gleitender Durchschnitt der vorherigen Periode

C_t: Endwert der betrachteten Periode

SF = 2/ (n + 1) Glättungsfaktor (Smoothing Factor) aus der Periodenlänge

dabei ist n die Periodenlänge

oder SF= α mit 0 < α < 1

Beim exponentiellen gleitenden Durchschnitt (Exponential Moving Average – EMA) fließt immer die gesamte vorhandene Datenpunkt-Datenreihe in die Berechnung ein. Die eingestellte Periodenlänge dient lediglich der Ermittlung des Gewichtungsfaktors. Auch beim EMA wird dem aktuelleren Kurs ein höheres Gewicht beigemessen als dem jeweils älteren.

Druck und speicherbares Bild